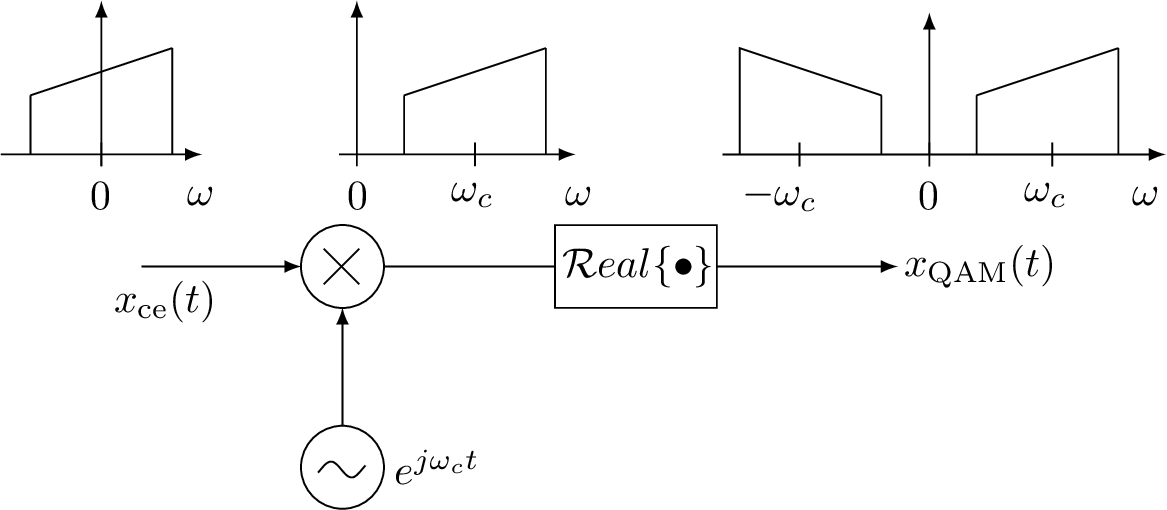
3.4 QAM Generation Using Complex-Valued Signals
It is mathematically convenient to use complex-valued signals when dealing with QAM. The two PAM signals compose the complex envelope
|
ce(t) = x_i(t) - j x_q(t),
which is a baseband complex-valued signal known to be the equivalent lowpass signal to the
passband .
Using the complex-valued signals notation, the upconversion to generate the QAM signal can then be represented by a complex exponential and the operation to extract the real part of the time-domain signal: which gives the same result as Eq. (3.2). Figure 3.5 illustrates the procedure.
To understand the spectra depicted in Figure 3.5, it is useful to interpret Eq. (3.4) in frequency domain. For this task, it is convenient to recall that the real part of a complex number can be obtained by and that . Applying these two results to Eq. (3.4) leads to Note from Eq. (3.5) that the real and imaginary parts of are the even and odd parcels of the corresponding parts of . This implies, as expected, that has Hermitian symmetry given that is real-valued.
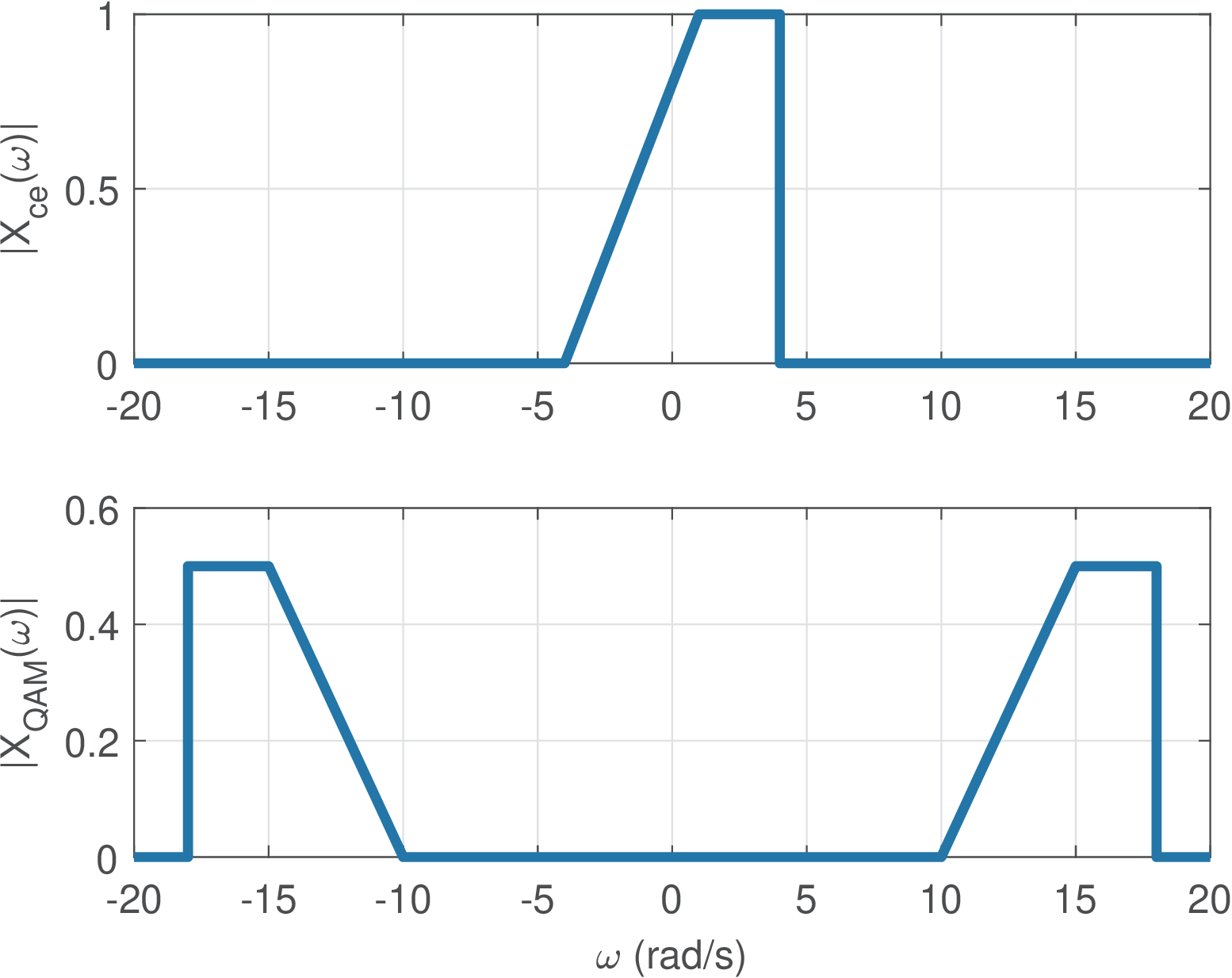
To provide more details on the spectra depicted in Figure 3.5, Figure 3.6 represents pictorially the spectrum magnitude ce(f)|x_i(t)x_q(t)X_ce(f)x_ce(t)X_QAM(f)|X_ce(f)| The complex notation also allows to represent a QAM symbol , where and are two PAM symbols. The generation of the QAM signal is similar to the process used for a PAM signal: upsampling followed by convolution with a shaping pulse. Listing 3.3 illustrates the process, which takes advantage of the capability of Matlab/Octave to deal with complex-valued signals (filter, convolve, etc.). The adopted shaping pulse is a “raised cosine”, which will be discussed in Section 4.5. 1%generate QAM signal centered at Fs/4 2M=16; %number of symbols 3constellat=ak_qamSquareConstellation(M); %QAM const. 4S=1000; %number of symbols 5ind=floor(M*rand(1,S)); %indices 6qamSymbols=constellat(ind+1); %sequence of random symbols 7L=8; %oversampling factor 8x=zeros(1,S*L); %pre-allocate space 9x(1:L:end)=qamSymbols; %complete upsampling operation 10p=ak_rcosine(1,L,'fir/normal',0.5,10); %raised cosine r=0.5 11yce=conv(p,x); %complex env.: convolution by shaping pulse 12%modulate by carrier at pi/2 rad that corresponds to Fs/4 13n=0:length(yce)-1; %"time" axis 14z=real(yce .* exp(j*pi/2*n)); %transmitted signal The complex envelope was previously defined as because should lead to Eq. (3.2). Sometimes slightly different definitions are assumed: the summation in Eq. (3.2) is modified to a subtraction:
such that the complex envelope is defined with a summation:
in order to continue having . The alternative Eq. (3.6) suggests defining a QAM symbol as and will be used hereafter. In this case, the QAM generation of Figure 3.3 multiplies by instead of . These latter definitions are assumed hereafter. Figure 3.6 uses Fourier transforms, but similar result holds for PSDs. In fact, it can be inferred1 from Eq. (F.34) that the average power of the real bandpass signal differs from the average power ce = E[|x_ce(t)|^2]x_ce(t) This is valid not only for QAM but for other bandpass signals obtained by upconverting a complex envelope. The factor of 2 also appears when modeling bandpass noise (or random signals, in general), which guarantees that signal to noise ratios are the same when representing bandpass signals by their corresponding lowpass complex envelopes. |