6.3  DMT Modulation via Matlab/Octave Code

In DMT, the channel partition is obtained with a DFT (more specifically, with an FFT) of size $N$. Several QAM and PAM symbols are grouped to create a DMT symbol represented by a vector Xk with $N$ elements $X[k],k\; =\; 0,\dots ,N\; -\; 1$, which is interpreted as in frequency domain. Conceptually, the subcarriers (sinusoids) are scaled by the elements of $X$ via an inverse FFT, as in Eq. (D.21), to obtain the time-domain samples xn. For example, the first element $X[0]$ of this vector is the substream information that will be transmitted at the DC tone ($k\; =\; 0$ in Eq. (D.41)).

In Matlab/Octave the modulation can be done with xn=ifft(Xk), but it is convenient to use an orthonormal definition of the pair FFT / IFFT, as explained via Eq. (D.44).

Before sending the time-domain samples to the DAC chip, the DMT modulator places a copy of the $L_{}$

cp$lastsamplesoftheIFFToutput\mathsf{\text{xn}}beforethefirstsampleof\mathsf{\text{xn}},creatinga“prefix″.Thesesamplesarecalled\mathit{\text{cyclic prefix}}(CP)andtheirimportancewillbeexplainedlaterinthischapter.Forexample,if$N=4$and\mathsf{\text{xn=[1 2 3 4]}},\; theadoptionofaCPof$L_cp=2$sampleswouldcreatethesignal\mathsf{\text{[3 4 1 2 3 4]}},while$L_cp=3$wouldleadto\mathsf{\text{[2 3 4 1 2 3 4]}}.TheminimumlengthofCP$L_cp$isthechannel\mathit{\text{dispersion}}$D$.$

Figure 6.1 depicts a DMT system. The FEQ block is the frequency equalizer that, for each tone, compensates the effect of the channel $H[k]$. Given an estimate $Ĥ[k]$ of the channel and eventually of the noise, the role of a FEQ algorithm to remove the deleterious influence of the channel. This can be done by multiplying each received symbol $Y_k$ by $1∕Ĥ[k]$.

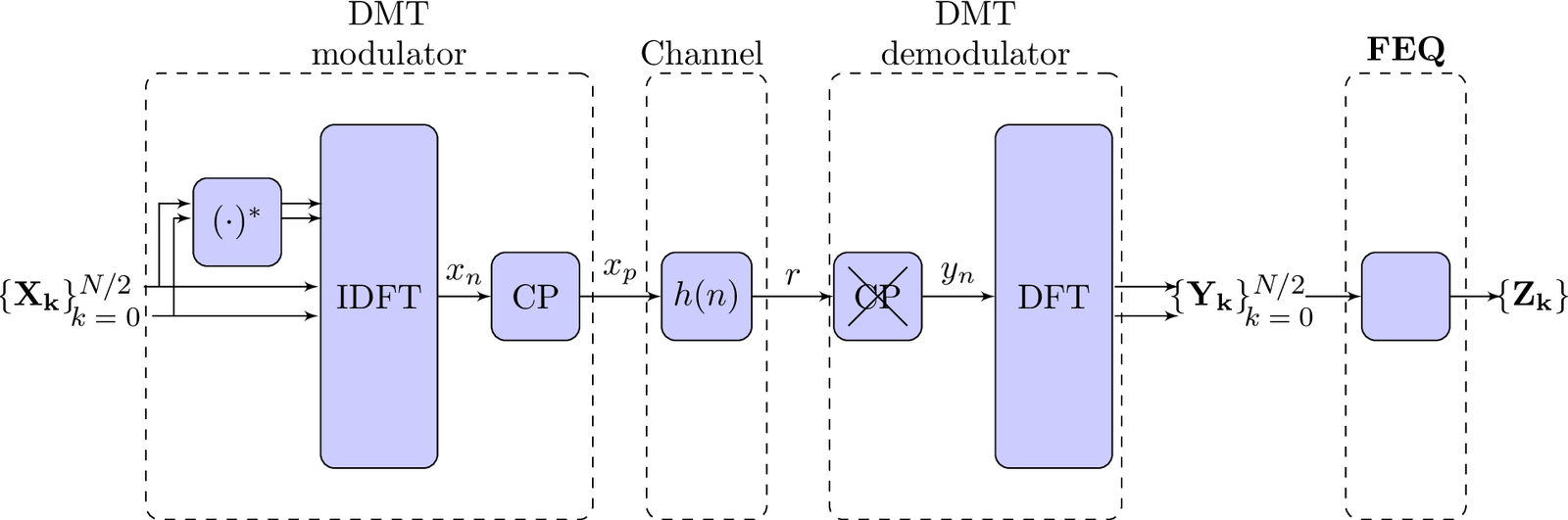
Because the system is designed such that the tones are independent, the fundamental DMT equation is

where $H_k$ and $N_k$ are the channel frequency response and noise at the $k$-th tone, respectively. This equation is valid under the assumption of a perfect channel partition.

Listing 6.1 shows how to transmit one DMT symbol using IFFT / FFT over a channel with impulse response $h[n]\; =\; 0.6\delta [n]\; +\; 1.2\delta [n\; -\; 1]\; +\; 0.3\delta [n\; -\; 2]$, which corresponds to a dispersion of $D\; =\; 2$ samples. In this case, it was adopted $L_{}$

cp=2$andtheresultofthecommand\mathsf{\text{Zk-Xk}}indicatesthatthetransmittedsymbolsareproperlyrecovered.$

1%Transmit a single DMT symbol with the channel relaxed 
2N=4 %number of FFT points 
3h=[0.6 1.2 0.3] %channel impulse response 
4Hk = fft(h,N) %find the channel freq. response at tone frequencies 
5Gk = 1 ./ Hk %frequency equalizer (FEQ): assume a perfect estimate 
6Xk=[-1 -1-1j 3 -1+1j] %DMT symbol, transmitted information 
7xn=ifft(Xk)*sqrt(N)  %adopt orthonormal FFT (Parseval applies) 
8xp=[xn(N-1) xn(N) xn]  %add cyclic prefix with Lcp=2 samples 
9r=conv(xp,h) %transmit over channel via linear convolution 
10yn=r(3:6)    %take cyclic prefix out 
11Yk=fft(yn)/sqrt(N)  %an orthonormal FFT has been adopted 
12Zk = Yk .* Gk  %estimated symbols, after FEQ, compare with Xk

Note in Listing 6.1 that a unitary (orthonormal) IFFT / FFT pair was used for modulation and demodulation. This is not strictly required and any valid DFT pair could be used, given that the output and input powers will be controlled by the analog front end electronics.

Note that, besides its usage for demodulation, the FFT is also adopted in Listing 6.1 to obtain the values Hk of the channel frequency response. These values correspond to sampling the channel DTFT and, to be properly estimated, the FFT normalization factors are $\alpha \; =\; 1$ and $\beta \; =\; 1∕N$, as explained in Eq. (D.44).

If the channel frequency response is 0 at some tone, it is not possible to send information via this tone. Recalling Eq. (E.53), if the channel has $h[n]\; =\; 0.6\delta [n]\; +\; 0.9\delta [n\; -\; 1]\; +\; 0.3\delta [n\; -\; 2]$, its system function is $H(z)\; =\; 0.6\; +\; 0.9z^{-1}+\; 0.3z^{-2}$, which has a zero gain at the Nyquist frequency. Listing 6.1 can be modified to use this channel and demonstrate that the information sent at tone $k\; =\; 2$ in this case cannot be recovered. Similarly, a channel with $H(z)\; =\; 0.6\; -\; 0.6z^{-1}$ has a zero gain at DC and the tone $k\; =\; 0$ should not be used in this case.

Listing 6.2 shows how to consecutively transmit two DMT symbols, indicating how the channel memory must be taken into account when using the routine filter in Matlab/Octave, as discussed in Application E.7.

1%transmit two DMT symbols (first with the channel relaxed) 
2N=4 %number of FFT points 
3h=[0.2 0.3 0.9] %channel impulse response 
4D=length(h)-1; %channel dispersion 
5L=D; %cyclic prefix length (minimum recommended value) 
6Hk = fft(h,N) %channel freq. response 
7Gk = 1 ./ Hk %frequency equalizer (FEQ): perfect estimate 
8ch_memory = zeros(1,D);  %initial channel memory zeroed 
9%Transmit 1st DMT symbol 
10Xk=[-1 -1-j 3 -1+j] %DMT symbol, transmitted information 
11xn=ifft(Xk)*sqrt(N)  %adopt orthonormal FFT 
12xp=[xn(N-L+1:end) xn]  %add cyclic prefix with L samples 
13[r,ch_memory]=filter(h,1,xp,ch_memory)%update channel mem. 
14yn=r(L+1:end)    %take CP out 
15Yk=fft(yn)/sqrt(N)  %an orthonormal FFT has been adopted 
16Zk = Yk .* Gk  %estimated symbols, after FEQ 
17ErrorInSymbols1 = Xk-Zk %check if symbols were recovered 
18%Transmit 2nd DMT symbol 
19Xk=[3 2-j 7 2+j] %info to be transmitted at 2nd symbol 
20xn=ifft(Xk)*sqrt(N)  %adopt orthonormal FFT 
21xp=[xn(N-L+1:end) xn]  %add cyclic prefix with L samples 
22[r,ch_memory]=filter(h,1,xp,ch_memory)%update channel mem. 
23yn=r(L+1:end)    %take CP out 
24Yk=fft(yn)/sqrt(N)  %an orthonormal FFT has been adopted 
25Zk = Yk .* Gk  %estimated symbols, after FEQ 
26ErrorInSymbols2 = Xk-Zk %check if symbols were recovered

Observe that X in Listing 6.1 has the required Hermitian symmetry to generate a real-valued DMT signal.

Assuming the sampling frequency (the rate that the transmitted DAC chip works) is $F_s$, the DFT tone spacing is ${\mathrm{\Delta }}_f=F_s∕N$ as illustrated in Table D.6. Hence, the carrier frequency of the $k$-th tone is given by Eq. (D.41): $f_k=\; k{F}_s∕N$.

While some standardized OFDM systems use the same number $b_k$ of bits for all tones, DMT-based DSL systems for example allocate more bits to tones with larger SNR. In other words, for DSL, $b_k$ is proportional to ${\mathrm{\text{SNR}}}_k$. The process of choosing $b_k$ is known as bit-allocation and will be discussed later. Before that, Listing 6.3 shows details about DMT with a given bitloading and the use of distinct constellations.

1N=8 %number of FFT points 
2h=[2 1 0 3]; %channel impulse response 
3%bitloading is [1, 2, 3, 3, 2] bits per symbol 
4%1) Design constellations 
5M = 2; pamconstM2 = -(M-1):2:M-1; %2-PAM 
6M = 4; pamconstM4 = -(M-1):2:M-1; %4-PAM 
7M = 4; qamconstM4 = ak_qamSquareConstellation(M); %4-QAM 
8M = 8; qamconstM8 = ak_qamSquareConstellation(M); %8-QAM 
9%Bitstream is B={0 11 101 100 10} 
10X0 = pamconstM2(bin2dec('0')+1); %find the symbol 
11X1 = qamconstM4(bin2dec('11')+1); 
12X2 = qamconstM8(bin2dec('101')+1); 
13X3 = qamconstM8(bin2dec('100')+1); 
14X4 = pamconstM4(bin2dec('10')+1); 
15X5 = conj(X3);  %impose the Hermitian symmetry 
16X6 = conj(X2); 
17X7 = conj(X1); 
18%Compose DMT symbol to be modulated and transmitted: 
19Xk=[X0 X1 X2 X3 X4 X5 X6 X7] 
20L = 3; %length of cyclic prefix = channel dispersion 
21xn=ifft(Xk)*sqrt(N)  %adopt orthonormal FFT 
22xp=[xn(N-L+1:N) xn]  %add cyclic prefix (CP) 
23r=conv(xp,h) %transmit: convolve with channel response h 
24yn=r(L+1:L+N) %take CP out and keep N information samples 
25Yk=fft(yn)/sqrt(N)  %an orthonormal FFT has been adopted 
26Hk=fft(h,N);%channel frequency response with N-points FFT 
27Gk = 1 ./ Hk %frequency equalizer FEQ 
28Zk = Yk .* Gk  %decoded symbols 
29%discard negative frequencies and demodulate 
30b0 = dec2bin(ak_pamdemod(real(Zk(1)),2)) 
31b1 = dec2bin(ak_qamdemod(Zk(2),4)) 
32b2 = dec2bin(ak_qamdemod(Zk(3),8)) 
33b3 = dec2bin(ak_qamdemod(Zk(4),8)) 
34b4 = dec2bin(ak_pamdemod(real(Zk(5)),4)) 
35receivedBitstream=[b0 ' ' b1 ' ' b2 ' ' b3 ' ' b4] 
36disp('Transmitted bitstream was B={0 11 101 100 10}')

The next section discusses how the rate can be calculated in multicarrier systems.