3.6  Quadrature (or IQ) Sampling

Quadrature (or IQ) sampling is the combined process of simultaneously digitizing the in-phase (I) and the quadrature (Q) signals. As depicted in Figure 3.12, this process requires a pair of mixers for generating the cosine and sine to obtain the I and Q components, respectively. The PLL and VCO aim at providing a stable signal to the 90 degree phase shifter. This figure also shows two DDCs (see Application 1.7).

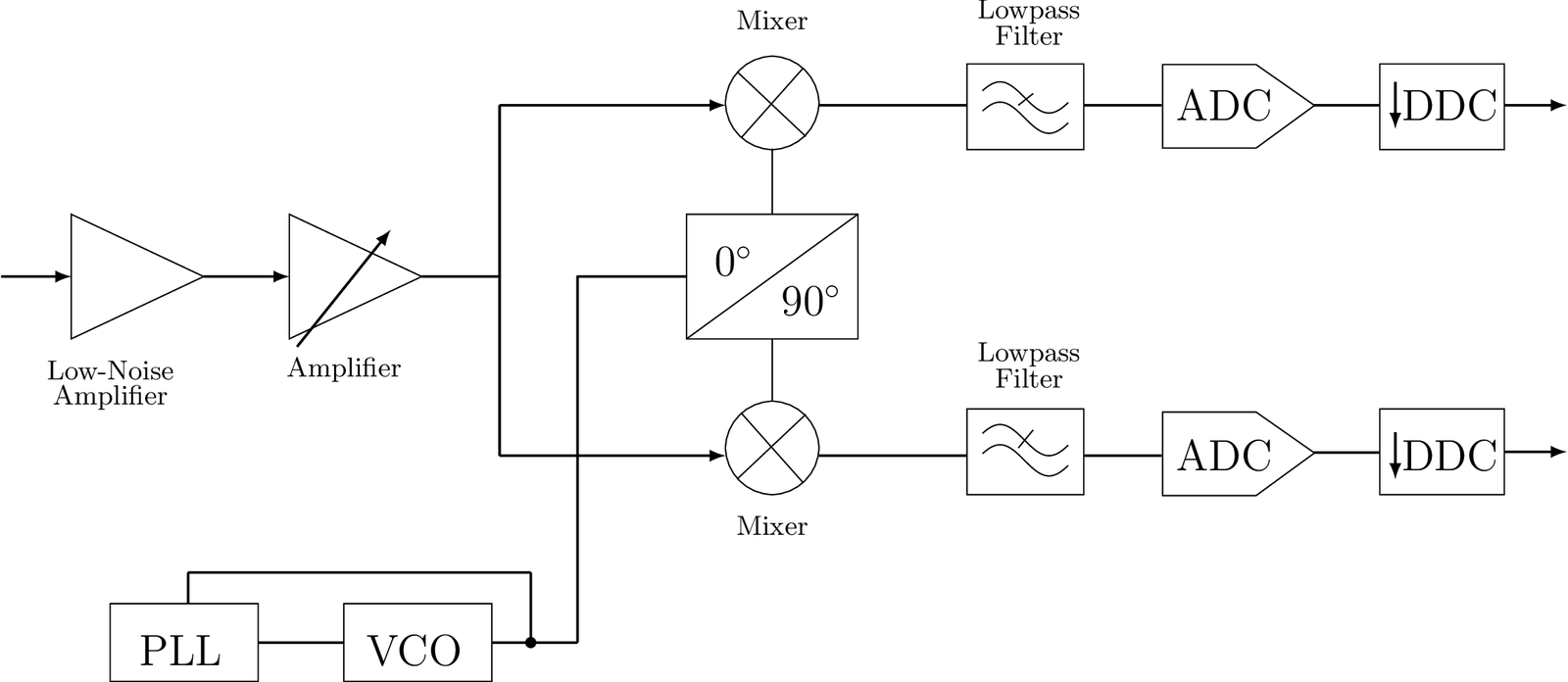
Quadrature sampling is sometimes referred to as quadrature demodulation, particularly when used to downconvert a bandpass signal to baseband. However, this term can be misleading in contexts where the goal is not full demodulation, but rather to shift or isolate a specific frequency band for further processing. For example, quadrature sampling was used to obtain the signal with spectrum depicted in Figure 1.7, but in this case the AM signals are not necessarily demodulated in this sampling process. To avoid ambiguity, we adopt the term quadrature sampling throughout this text.

Another observation is that quadrature sampling should not be confused with passband sampling (also called undersampling and IF sampling), which is discussed in Section E.5.5.

As mentioned, Eq. (C.30) provides a lower bound of $F_s$ when the signal $x(t)$ is real-valued and baseband. When complex signals can be used, the sampling theorem expressed in Eq. (C.30) can be specialized. A band-limited complex-valued and analytic signal $x_{\mathrm{\text{bb}}}(t)$ can be reconstructed from its sampled version when the complex-valued samples are taken at rate

with $x_{\mathrm{\text{bb}}}(t)$ having negligible energy outside the frequency range $[0,F_{\mathrm{\text{max}}}]$. Given that the signal bandwidth is $\mathrm{\text{BW}}=F_{\mathrm{\text{max}}}$, Eq. (3.10) can also be written as $F_s>\mathrm{\text{BW}}$, as previously stated in Eq. (E.39) (and further detailed in Table 4.3).

Considering that a complex-valued sample requires two real-valued samples, Eq. (3.10) does not contradict Eq. (C.30). Both equations predict that more than two real values per Hertz need to be used to represent a band-limited signal.