2.13 Simple example of M-PAM simulation over AWGN
This section starts by analyzing M-PAM transmission over AWGN using a simulation on Matlab/Octave. The reader is encouraged to run and understand the simulation before proceeding.
The function ak_waveformSimulationOfPAMInAWGN.m listed below presents a simple PAM simulation. The channel simply adds Gaussian noise (no filtering, the channel impulse response is ) and the receiver makes its decision based on a single sample, arbitrarily extracted from the middle of each symbol interval.
1function [ber,ser,SNRdB] = ... 2 ak_waveformSimulationOfPAMInAWGN(numberOfBytes,... 3 oversample, M, noisePower) 4%[ber,ser,SNRdB] = ... 5% ak_waveformSimulationOfPAMInAWGN(numberOfBytes,... 6% oversample, M, noisePower) 7%Inputs: 8%numberOfBytes -> number of bytes to be transmitted 9%oversample -> oversampling factor 10%M -> modulation order (number of constellation symbols) 11%noisePower -> noise power 12%Outputs: 13%ber -> bit error rate 14%ser -> symbol error rate 15%SNRdB -> signal to noise ratio in dB 16b=log2(M); %number of bits per symbol 17bytesTx = floor(256*rand(1,numberOfBytes)); %random bytes 18symbolIndicesTx = ak_sliceBytes(bytesTx, b); 19%constellation = pammod(0:M-1, M); %see the constelllation 20symbols = pammod(symbolIndicesTx,M); % modulate 21%% 1) Convert symbols into a waveform: 22p = ones(1,oversample); %define a simple shaping pulse 23p = p / (mean(p.^2)); %make sure pulse has unitary power 24numSymbols = length(symbols); %number of symbols 25waveform = zeros(1,numSymbols*oversample); %pre-allocate 26waveform(1:oversample:end) = symbols; 27waveform = filter(p,1,waveform); % Pulse shaping filtering 28%% 2) Send waveform through AWGN channel 29n = sqrt(noisePower)*randn(size(waveform));%generate noise 30r = waveform + n; %add transmitted signal and noise 31SNRdB=10*log10(mean(waveform.^2)/mean(n.^2));%estimate SNR 32%% 3) Implement simple receiver: 33initialSample = oversample/2; %sample in middle of symbol 34receivedSymbols = r(initialSample:oversample:end); %sample 35symbolIndicesRx = pamdemod(receivedSymbols, M); 36bytesRx = ak_unsliceBytes(symbolIndicesRx, b); 37ser = ak_calculateSymbolErrorRate(symbolIndicesTx, ... 38 symbolIndicesRx); %estimate SER 39ber = ak_estimateBERFromBytes(bytesTx, bytesRx); % BER
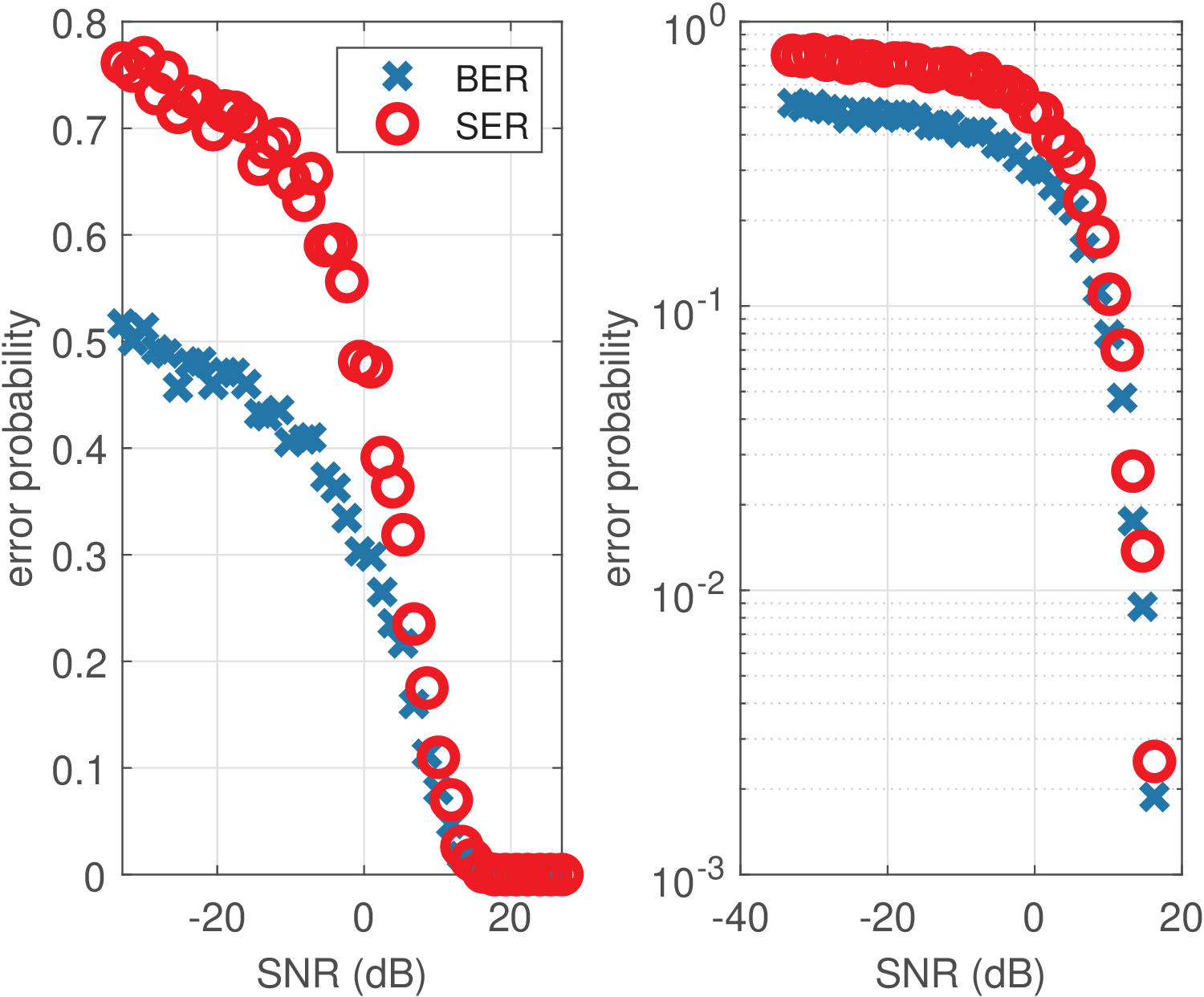
Using this code and varying the noise power, the error probabilities in Figure 2.27 are obtained.
In Figure 2.27, the plot at the right is a version using semilogy.m of the one at the left. Note that Matlab/Octave cannot show the log of 0 and the right abscissa is smaller than the left one because there are zero errors for SNR larger than approximately 17 dB. To reliably estimate the SER for larger SNR, the number of transmitted symbols would have to be increased.