Advanced: Sampling and Signal Reconstruction Revisited

3.5 Advanced: Sampling and Signal Reconstruction Revisited

Having established the fundamentals of convolution and Fourier transforms, it is possible now to sketch a proof of the sampling theorem (Theorem 1) without difficulties.

3.5.1 A proof sketch of the sampling theorem

Sampling a signal $x (t)$ at each $T_{s}$ seconds (periodic and uniform sampling) can be modeled as the multiplication of $x (t)$ by a periodic function $p (t)$ with fundamental period $T_{s}$ . For example, $p (t)$ can be a train of pulses with duty cycle $T_{1}$ . However, it is mathematically convenient³ to adopt an impulse train

p (t) = \sum_{k = - \infty}^{\infty} δ (t - k T_{s}),

(3.14)

which allows to model the sampled signal as

x_{s} (t) = x (t) p (t) = \sum_{k = - \infty}^{\infty} x (k T_{s}) δ (t - k T_{s}),

(3.15)

as anticipated in Eq. (1.31).

From Eq. (3.15) and the Fourier convolution property discussed in Section 3.4.7, the Fourier transform of $x_{s} (t)$ is

X_{s} (f) = X (f) * P (f),

(3.16)

where $X (f) = F {x (t)}$ and $P (f) = F {p (t)}$ is another impulse train, but in frequency domain. As indicated by Eq. (A.61), the impulses in $P (f)$ are spaced by $F_{s} = 1 ∕ T_{s}$ and have area $F_{s} = 1 ∕ T_{s}$ .

The convolution of $X (f)$ with the impulses in $P (f)$ creates infinite replicas of $X (f)$ at frequencies values that are multiples of $F_{s}$ as depicted in Figure 3.11. As well-discussed in textbooks, if $F_{s}$ is not sufficiently large, these replicas will overlap and create aliasing. But in case $F_{s} > 2 F_{max}$ , all replicas are “perfect” copies of $X (f)$ scaled by $T_{s}$ . The original spectrum can then be recovered by keeping one replica and eliminating the others. This filtering procedure is assumed here to be done with an ideal lowpass filter with bandwidth $BW = F_{max}$ and gain $T_{s}$ . This ideal filter will then cancel the undesired replicas of $X_{s} (f)$ and recover $X (f)$ using precisely the scaling factor $T_{s}$ .

Figure 3.11: Spectrum $X_{s} (f)$ of a sampled signal $x_{s} (t)$ obtained by the convolution between $X (f)$ and $P (f)$ as indicated in Eq. (3.16).

In summary, a lowpass signal $x (t)$ with maximum frequency $F_{max}$ , can be perfectly reconstructed from its sampled version $x_{s} (t)$ if the sampling frequency obeys $F_{s} > 2 F_{max}$ (Theorem 1) and the reconstructed signal $\hat{x} (t) = x (t)$ is obtained by passing $x_{s} (t)$ through an ideal lowpass filter with frequency response $H (f)$ having gain $T_{s}$ over the passband.

The spectrum $\hat{X} (f)$ of $\hat{x} (t)$ corresponds to $\hat{X} (f) = X_{s} (f) H (f)$ . The multiplication of $X_{s} (f)$ by $H (f)$ in frequency-domain corresponds to the convolution of $x_{s} (t)$ with the filter’s impulse response $h (t) = F {H (f)}$ . From Eq. (A.54) and the duality property, $h (t) = sinc (t ∕ T_{s})$ in this case. Hence, this convolution is written as

\hat{x} (t) = x_{s} (t) * h (t) = \sum_{n = - \infty}^{\infty} x_{s}^{a} (n T_{s}) sinc (\frac{t}{T_{s}} - n),

(3.17)

which corresponds to the convolution of the scaled sinc $h (t)$ with impulses⁴ of area $x_{s}^{a} (n T_{s})$ . The time shift by $n$ in Eq. (3.17) positions the sincs at $n T_{s}$ , and was discussed in Example 1.5.

Eq. (3.17) represents the reconstruction of a band-limited signal by the sinc interpolation of its samples and is called the Whittaker-Shannon interpolation formula .

Hence, when the sampling theorem is obeyed, the whole chain is as follows (the signals are depicted with their associated power in parenthesis as in Block (1.69)):

\underset{(P_{c})}{x (t)} \to sampling \to \underset{(P_{s})}{x_{s} (t)} \to S ∕ D \to \underset{(P_{d})}{x [n]} \to D ∕ S \to \underset{(P_{s})}{x_{s} (t)} \to h (t) \to \underset{(P_{c})}{\hat{x} (t)} = x (t)

(3.18)

where $h (t) = sinc (t ∕ T_{s})$ is the discussed ideal filter.

Using the notation suggested by Block (3.18), the samples $x (n T_{s})$ were converted to areas $x_{s}^{a} (n T_{s})$ , which are converted to $x [n] = x_{s}^{a} (n T_{s})$ . Hence, Eq. (3.17) can be conveniently rewritten as

\hat{x} (t) = x_{s} (t) * h (t) = D/S {x [n]} * h (t) = \sum_{n = - \infty}^{\infty} x [n] sinc (\frac{t}{T_{s}} - n) .

(3.19)

3.5.2 Energy and power of a sampled signal

The squared of the continuous-time impulse $δ^{2} (t)$ is not defined. This creates a problem when one considers the energy or power of $δ (t)$ . When $δ (t)$ is interpreted as a pulse $p (t)$ with unit area and amplitude $1 ∕ Δ$ , one can argue that when $lim_{Δ \to 0}$ as in Eq. (A.121), the resulting area of the squared pulse $p^{2} (t)$ is $1 ∕ Δ$ , which leads to $δ^{2} (t) = \infty$ . However, this would not be mathematically rigorous given that $δ (t)$ is a distribution. Hence, the following route is taken here: instead of defining new transformations⁵ on the distribution $δ (t)$ , the instantaneous power of a sampled signal $x_{s} (t)$ is defined as the instantaneous power of its equivalent discrete-time signal $x [n]$ obtained via a S/D conversion, normalized by the associated $T_{s}$ , i. e.

P_{s} \overset{def}{=} \frac{P_{d}}{T_{s}} .

(3.20)

For example, the pulse train of Eq. (3.14) has average power $P_{s} = 1 ∕ T_{s}$ because when converted to discrete-time its power is $P_{d} = 1$ .

The same reasoning can be applied to sampled signals for which the independent variable is not $t$ . The Fourier transform $P (f) = {p (t)}$ of Eq. (3.14) has power $1 ∕ T_{s}$ because its discrete-frequency version has power $1 ∕ {T_{s}}^{2}$ and the normalizing factor is $1 ∕ T_{s}$ in this case. Note that, with this definition of instantaneous power of a sampled signal, the power of the impulse trains $p (t)$ and $P (f)$ are the same, as expected from Eq. (A.52).

3.5.3 Energy / power conservation after sampling and reconstruction

With the help of Eq. (3.19), it is possible to sketch a proof for Eq. (1.71), which is valid when the sampling theorem is obeyed.

Eq. (3.19) states that any band-limited signal $x (t)$ can be represented by its samples $x [n]$ . The interest here is to relate their respective power values $P_{c}$ and $P_{d}$ . Assuming $x (t)$ is an energy signal and from Eq. (A.28), its energy $E_{c}$ can be written as

E_{c} = \int_{- \infty}^{\infty} | x (t) |^{2} d t = \int_{- \infty}^{\infty} {| ∑_{n = - \infty}^{\infty} x [n] sinc (t ∕ T_{s} - n) |}^{2} d t = T_{s} \sum_{n = - \infty}^{\infty} | x [n] |^{2} = T_{s} E_{d},

(3.21)

where $E_{d}$ is the energy of $x [n]$ . A similar reasoning can be applied to power signals. Rewriting Eq. (1.23) with $Δ t = N T_{s}$ leads to

\begin{array}{l} P_{c} & = lim_{N \to \infty} [\frac{1}{(2 N + 1) T_{s}} \int_{- N T_{s}}^{N T_{s}} {| \sum_{n = - N}^{N} x [n] sinc (t ∕ T_{s} - n) |}^{2} d t] \\ = lim_{N \to \infty} [\frac{T_{s}}{(2 N + 1) T_{s}} \sum_{n = - N}^{N} | x [n] |^{2}] \\ = P_{d} . & (3.22) \end{array}

From Eq. (3.22) and Eq. (3.20), Block (3.18) can be simplified as

\underset{(P)}{x (t)} \to sampling \to \underset{(P ∕ T_{s})}{x_{s} (t)} \to S ∕ D \to \underset{(P)}{x [n]} \to D ∕ S \to \underset{(P ∕ T_{s})}{x_{s} (t)} \to h (t) \to \underset{(P)}{\hat{x} (t)} = x (t),

(3.23)

where $P = P_{c} = P_{d}$ .

3.5.4 Sampling theorem uses a strict inequality

Some authors state this theorem as $F_{s} \geq 2 F_{max}$ , but in this case $F_{max}$ would have to be interpreted as the frequency for which $X (f)$ does not have a discrete frequency component $δ (f - F_{max})$ . The confusion often arises when textbooks pictorially represent $X (f)$ with a triangle shape as in Figure 3.11 and, in this case, $F_{max}$ is the “maximum” but $X (F_{max}) = 0$ such that $F_{s} \geq 2 F_{max}$ “works”. However, as the exercise of Eq. (1.33) suggests, it is not guaranteed to reconstruct a cosine of frequency $f_{c}$ if one takes its samples at rate $F_{s} = 2 f_{c}$ .

Another source of confusion with respect to $F_{s} \geq 2 F_{max}$ or $F_{s} > 2 F_{max}$ is that when processing a signal sampled at $F_{s}$ with an FFT, the maximum frequency is the so-called Nyquist frequency $F_{s} ∕ 2$ of Table 1.5. Taking that $F_{max} = F_{s} ∕ 2$ , it seems reasonable to adopt $F_{s} \geq 2 F_{max}$ . Note however that the FFT bin corresponding to the Nyquist frequency is representing all signal components within its width $Δ_{f}$ and that, unless $X (f)$ has a discrete frequency component $δ (f - F_{max})$ to create ambiguity as exemplified in Eq. (1.33), there is no major practical issue.

3.5.5 Undersampling or passband sampling

Most digital signal processing (DSP) systems are designed to combat aliasing but there are exceptions. In digital communications, it is common to use aliasing to lower the frequency of a signal $x (t)$ in an operation known as undersampling or passband sampling. Among other conditions, $x (t)$ has to be a passband signal with spectrum centered at (a relatively high) frequency $f_{c}$ , but with (a relatively small) bandwidth $BW < f_{c}$ , such that $F_{s} > 2 BW$ . In this case, even if $F_{s} < 2 f_{max}$ , where the maximum frequency is $f_{max} = f_{c} + 0.5 BW$ , $x (t)$ can still be reconstructed from a replica of its spectrum that was shifted in frequency.

For example, consider a passband signal $x (t)$ with spectrum $X (f)$ with $BW = 25$ Hz and center frequency $f_{c} = 70$ Hz, as depicted in Figure 3.12. This signal has $f_{max} = f_{c} + 0.5 BW = 82.5$ Hz and using the sampling theorem as applied to lowpass signals one would be compeled to use $F_{s} > 2 \times 82.5 = 165$ Hz. However, using $F_{s} = 56$ Hz, for example, one can still recover the signal.

Figure 3.12: Passband signal with $BW = 25$ Hz and center frequency $f_{c} = 70$ Hz.

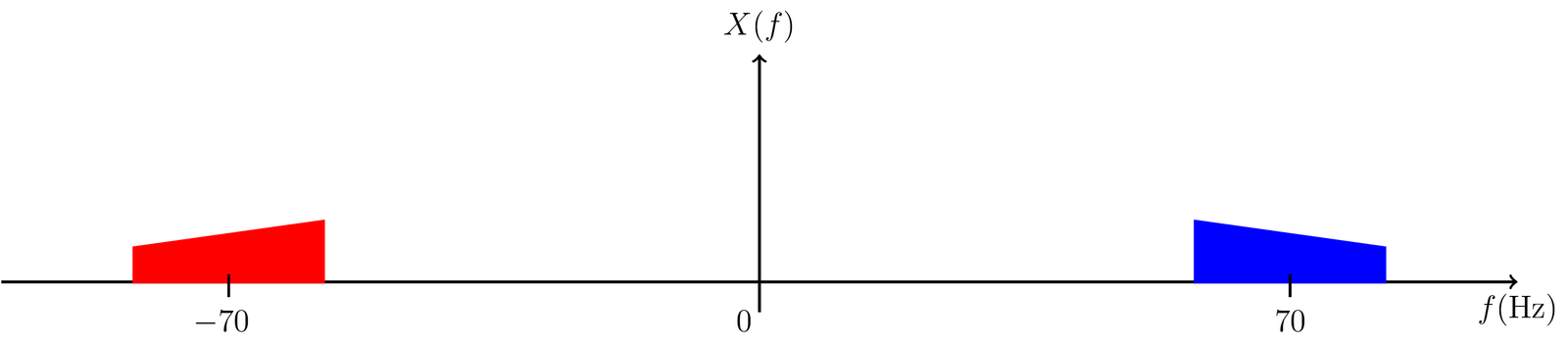
According to the classic model for the sampling operation, it corresponds to the convolution of $X (f)$ with an impulse train $P (f)$ such that $X_{d} (f) = X (f) * P (f)$ and $P (f)$ has impulses separated by $F_{s} = 56$ . Hence, the sampled signal has spectrum $X_{d} (f)$ as depicted in Figure 3.13.

Assuming $x (t)$ is real and $X (f)$ has Hermitian symmetry, any of the two “replicas” in Figure 3.12 could be used to reconstruct $x (t)$ . Similarly, any of the six (among the infinite) replicas that are shown in Figure 3.13 could be used to reconstruct $x (t)$ .

Figure 3.13: Result of sampling $X (f)$ in Figure 3.12 with $F_{s} = 56$ Hz, which places replicas at $f = \pm 14, \pm 42, \pm, 70, \pm 98, \dots$ , with only the first six shown in this figure.

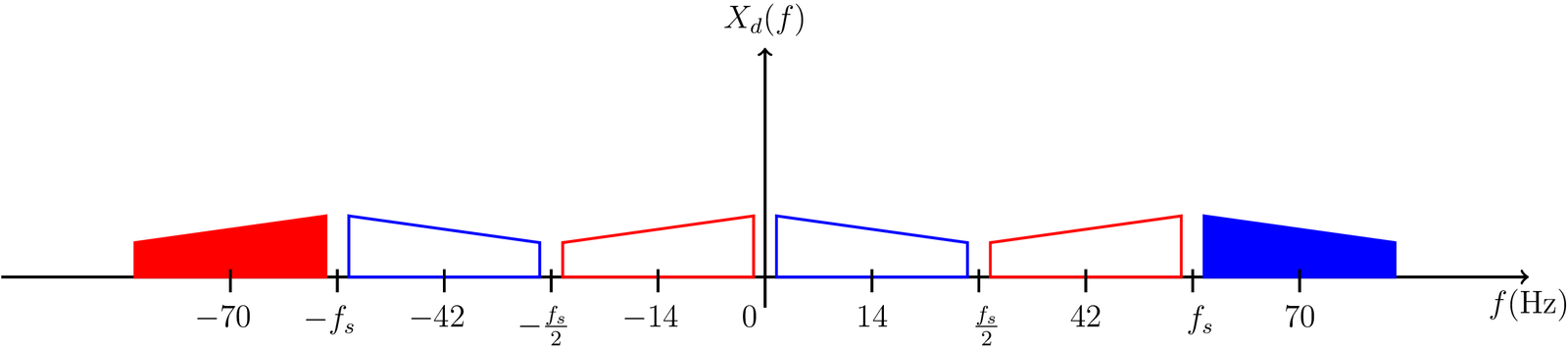
For example, placing an ideal lowpass filter with cutoff frequency $F_{s} ∕ 2$ would obtain a version of $x (t)$ corresponding to a frequency downconversion of its spectrum $X (f)$ from 70 to 14 Hz.

The theory about undersampling indicates the range of $F_{s}$ that can be used in each situation and can be found in DSP textbooks.⁶

3.5.6 Sampling a complex-valued signal

The sampling theorem (Theorem 1) assumed a real-valued signal, which consequently, allowed to assume the spectrum magnitude is even (symmetric). In the more general case of a complex-valued signal, the same principle of having spectrum replicas that cannot overlap is valid, but the “maximum positive frequency” is not enough to determine the minimum $F_{s}$ .

Figure 3.14 suggests an example where a complex-valued signal has spectrum $X (f)$ with support from $- 300$ to 100 Hz. A careless interpretation of the sampling theorem could lead to the erroneous conclusion that $F_{s} > 2 \times 100$ Hz suffices to avoid aliasing. But in this case $F_{s} > 400$ Hz is required to avoid the overlap of spectrum replicas. Figure 3.14 adopts $F_{s} = 450$ Hz.

Figure 3.14: Sampling with $F_{s} = 450$ Hz a complex-valued signal with non-symmetrical spectrum.

Stating the sampling theorem for complex-valued signals requires more elaborated definitions of bandwidth (this is discussed in Section 3.7.2.0). But Figure 3.14 (and Figure 3.11) indicate that an efficient strategy is to follow the basic principle of avoiding aliasing after convolving the original spectrum with the train of impulses spaced by $F_{s}$ .

3.5.7 Signal reconstruction and D/S conversion revisited

Similar to sampling, the D/S conversion can now be better understood. After that, the important topic of signal reconstruction is discussed.

D/S conversion revisited

When a discrete-time signal $x [n]$ with DTFT $X (e^{j Ω})$ is converted into a sampled signal $x_{s} (t)$ with Fourier transform $X_{s} (ω)$ via a D/S conversion, as discussed in Section 1.7.6, it has a frequency-domain description given by

X_{s} (ω) = X (e^{j Ω}) |_{Ω = ω T_{s}} = X (e^{jω T_{s}}) .

(3.24)

In other words, the value of $X_{s} (ω_{0})$ for a specific frequency $ω_{0}$ rad/s is obtained from $X (e^{j Ω_{0}})$ where $Ω_{0} = ω_{0} T_{s}$ rad, as dictated by Eq. (1.36).

The notation is such that the subscript in $X_{s} (ω)$ indicates the Fourier transform of a “sampled” signal or, alternatively, $X (e^{jω T_{s}})$ can be used. In both cases, the reader should have in mind that a sampled signal has a periodic spectrum.

Eq. (3.24) corresponds to scaling the abscissa of $X (e^{j Ω})$ , originally specified in rad, to create $X (e^{jω T_{s}})$ with an abscissa $ω = Ω F_{s}$ in rad/s. Figure 3.15 provides an example of the spectra involved in this D/S conversion.

Figure 3.15: Result of converting $x [n]$ with spectrum $X (e^{j Ω})$ into $x_{s} (t)$ with $X_{s} (ω) = X (e^{jω T_{s}})$ via a D/S conversion using $F_{s} = 10$ Hz.

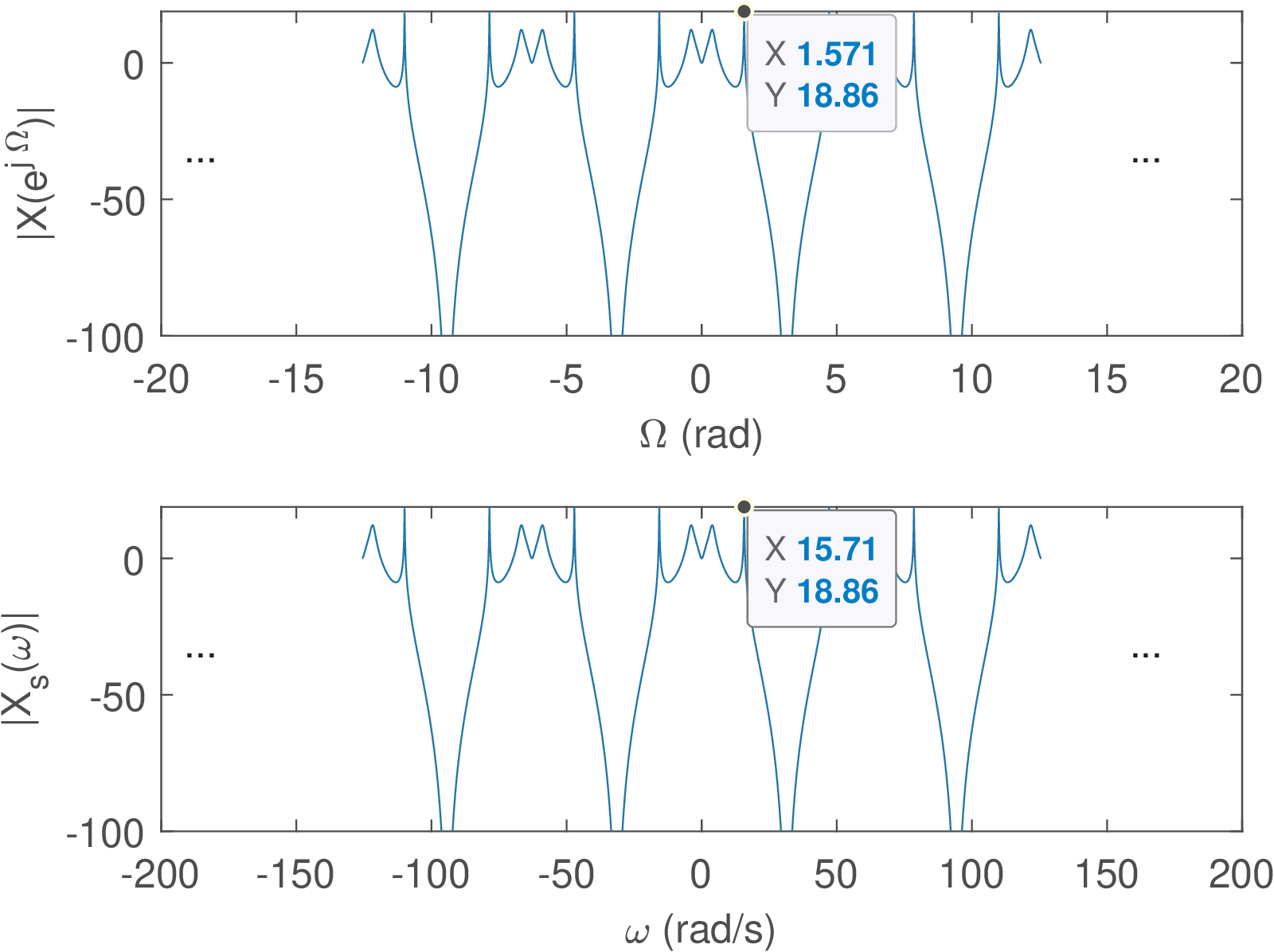
The datatips in Figure 3.15 highlight that the value $| X (e^{j Ω_{0}}) | = 18.86$ at $Ω_{0} = 1.571$ rad was converted to $| X (ω_{0}) |$ where $ω_{0} = Ω_{0} F_{s} = 15.71$ rad/s.

The replicas that occur in the spectrum of a sampled signal are located in Nyquist zones, which are intervals of $F_{s} ∕ 2$ when the frequency $f$ is specified in Hertz. For example, the first Nyquist zone is $[0, F_{s} ∕ 2 [$ , the second is $[F_{s} ∕ 2, F_{s} [$ and so on. When the frequencies $ω$ and $Ω$ are specified in rad/s and rad, the bandwidths of the Nyquist zones are $π F_{s}$ and $π$ , respectively.

In summary, $X_{s} (ω)$ inherits the periodicity of $X (e^{j Ω})$ in spite of the notation indicating it only by the subscript $s$ of “sampled”. Therefore, in some situations, it is convenient to denote the spectrum of $x_{s} (t)$ as $X (e^{jω T_{s}})$ , which indicates that the independent variable $ω$ is in rad/s and makes explicit that this spectrum is periodic. An alternative to describing the sampled-signal spectrum $X (e^{jω T_{s}})$ in rad/s is to use $ω = 2 πf$ and represent $X (e^{j 2 πf T_{s}})$ in Hz.

The adoption of a filter to eliminate or attenuate the periodic replicas of a sampled signal $X (e^{jω T_{s}})$ is discussed in the sequel.

Signal reconstruction

Digital signal processing systems that interface with the analog world typically require two analog filters: the anti-aliasing and reconstruction, as indicated in Figure 3.30.

The reconstruction process, which converts a sampled signal $x_{s} (t)$ into a continuous-time signal $x (t)$ , is mathematically modeled by convolving $x_{s} (t)$ with a signal $h (t)$ to obtain $x (t) = x_{s} (t) * h (t)$ . As discussed along the text, the signal $h (t)$ can be interpreted as the impulse response of a system and the reconstruction process can be pictorially depicted as:

x_{s} (t) \to h(t) \to x (t) .

(3.25)

When one starts with the discrete-time signal $x [n]$ , the D/A process has two stages: D/S conversion, that transforms the discrete-time $x [n]$ into a continuous sampled signal $x_{s} (t)$ and then processing (or “filtering”) with $h (t)$ to obtain $x (t)$ .

There are two important options for $h (t)$ :

Zero-order hold reconstruction: where $h (t) = u (t) - u (t - T_{s})$ is a pulse with duration $T_{s}$ and amplitude 1
Unitary energy reconstruction: where $h (t)$ has unitary energy $E = 1$ as, for example, the normalized pulse $h (t) = \frac{1}{\sqrt{T_{s}}} [u (t) - u (t - T_{s})]$

As illustrated in Figure 1.35, D/S followed by zero-order hold reconstruction is a simplified model for the actual process executed by a DAC chip. It is adopted here for simplicity. A consequence of ZOH is that Eq. (1.71) holds, and the power in continuous $P_{c}$ of $x (t)$ and discrete-time $P_{d}$ of $x [n]$ are the same.

In practice, the reconstruction process heavily depends on the respective analog filter and the DAC sampling frequency $F_{s}$ . It is often necessary to use $F_{s}$ higher than the one suggested by the sampling theorem, to simplify the job that must be done by the reconstruction filter $H (f) = F {h (t)}$ .

For a signal with approximate bandwidth BW, it is tempting to use $F_{s} = 2 BW$ , which is denoted as Nyquist sampling. In this case the signal is called critically-sampled and the reconstruction should be done by an ideal lowpass filter with passband from 0 to $F_{s} ∕ 2$ . Even when $F_{s} > 2 BW$ , the transition band of the reconstruction filter should be small enough to significantly attenuate the neighboring spectrum replicas of the sampled signal at the output of the D/S conversion.

Recall that the spectrum replicas of $X (e^{jω T_{s}})$ are located at multiples of $2 π F_{s}$ rad/s (see, e. g., Figure 3.15), which correspond to replicas at multiples of $F_{s}$ when considering $X (e^{j 2 πf T_{s}})$ with the frequency $f$ in Hz.

Figure 3.16 presents an extended version of Figure 1.36 that incorporates the filters $A (s)$ and $R (s)$ (these two analog filters are also indicated in Figure 3.30). While Figure 1.36 assumed ZOH reconstruction, Figure 3.16 illustrates the general case of an arbitrary reconstruction filter $h (t)$ .

Figure 3.16: Extended version of Figure 1.36 using an arbitrary reconstruction filter $h (t)$ and incorporating the filters $A (s)$ and $R (s)$ .

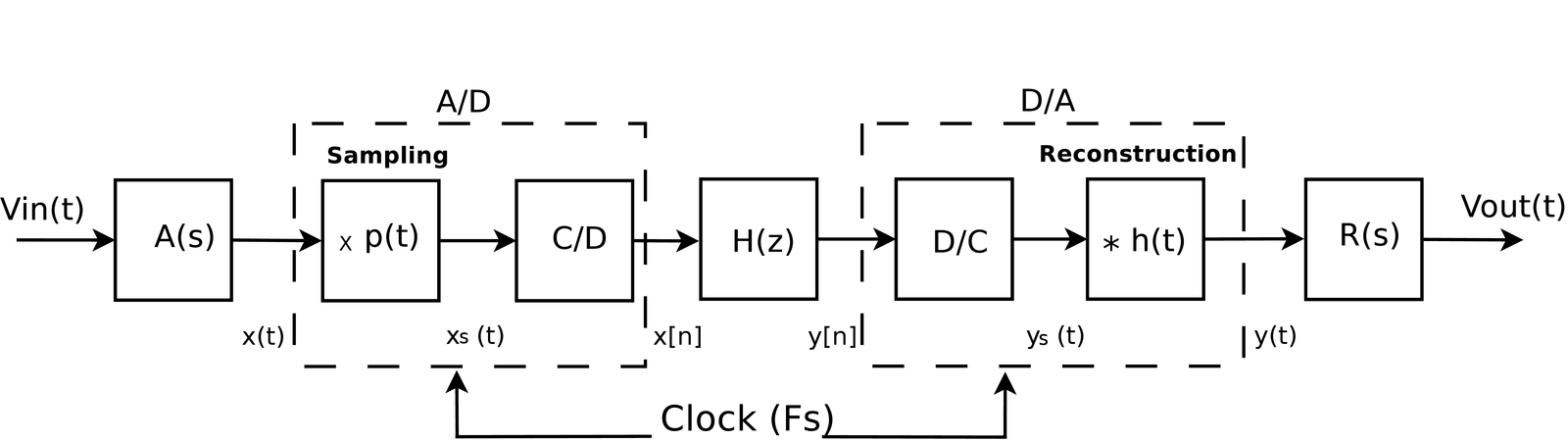
Note that there are two reconstruction filters in Figure 1.36, represented by $h (t)$ and $R (s)$ . Their effect could be combined in only one filter with impulse response $h_{r} (t) = h (t) * r (t)$ , where $r (t)$ is the inverse Laplace transform of $R (s)$ , but it is often pedagogical to distinguish them as follows.

The internal filter $h (t)$ represents the filtering process that occurs within a DAC chip. Modern DACs can already incorporate a sophisticated $h (t)$ , but is is assumed here that this is not the case, and $h (t)$ may implement ZOH or a filter with small order. The “external” reconstruction filter $R (s)$ complements $h (t)$ and provides improved rejection of the undesired spectrum replicas of $y_{s} (t)$ that may still be present in $y (t)$ . In summary, the main role of $h (t)$ is the conversion of the sampled signal $y_{s} (t)$ into an analog signal $y (t)$ , while $R (s)$ aims at achieving the specified level of performance with respect to filtering out the replicas in $y_{s} (t)$ . The following example illustrates how signal reconstruction can be challenging in practice.

Example 3.6. Examples of signal reconstruction. Figure 3.17 is the result of an example⁷ where a random signal $y [n]$ with $BW = 25$ kHz and $F_{s} = 200$ kHz, is converted to an analog signal $y (t)$ . The reconstruction is performed by a DAC followed by a 5-th order analog filter $H (f)$ , with cutoff frequency $f_{c} = BW$ . This analog filter combines the effects of $h (t)$ and $R (s)$ in Figure 3.16.

The top plot in Figure 3.17 shows the magnitude of the DTFT $Y (e^{2 π T_{s} f})$ of $y_{s} (t) = D/S {y [n]}$ , superimposed to the frequency response $| H (f) |$ of the reconstruction filter. The multiples of $F_{s}$ are identified in the grid of dashed lines. The bottom plot shows the magnitude of the resulting Fourier transform $Y (f) = F {y (t)}$ .

Figure 3.17: Reconstruction of a digital signal with $BW = 25$ kHz and $F_{s} = 200$ kHz using an analog filter with cutoff frequency $f_{c} = 25$ kHz.

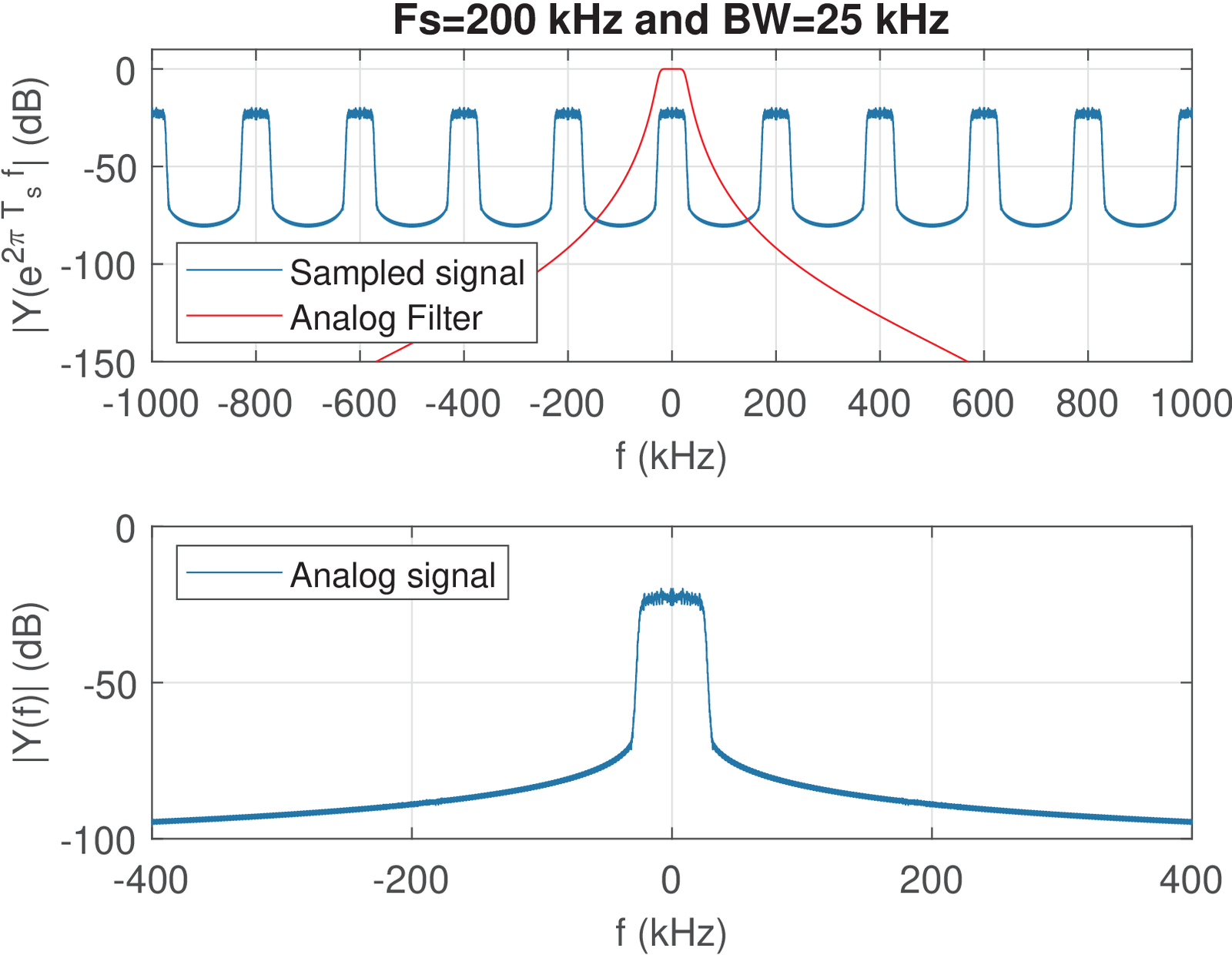
Figure 3.18 was obtained under the same conditions used for Figure 3.17 but the signal bandwidth increased from 25 to 80 kHz. In this case, the filter did not significantly attenuate the two spectrum replicas in $Y (e^{2 π T_{s} f})$ that are neighbors of the one centered at $f = 0$ . Thinking of an asymptotic Bode-diagram, one can expect the fifth-order $| H (f) |$ to drop at 6 dB/octave per pole and, from 80 to 160 kHz, reach $5 \times (- 6) = - 30$ dB. The replica centered at 200 kHz, for example, has its band starting at 120 kHz, and the reconstruction filter has an attenuation of only (approximately) 20 dB at 120 kHz.

Figure 3.18: Same as Figure 3.17, but for a signal with $BW = f_{c} = 80$ kHz. In this case, the reconstruction generates significant out-of-band power due to the spectrum replicas.

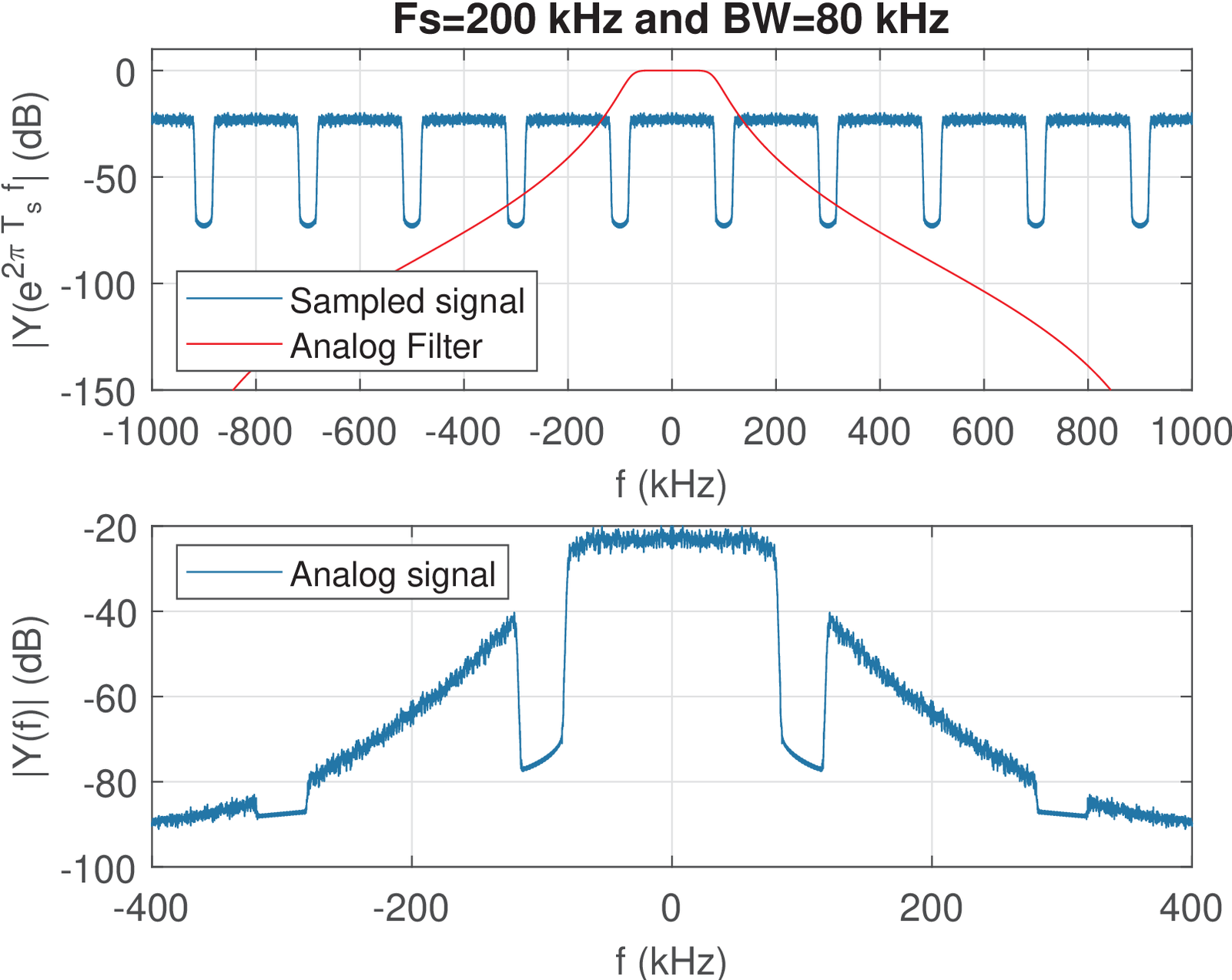
As illustrated by Figure 3.18, in practice, it is typically adopted a value for $F_{s}$ large enough due to the non-ideal reconstruction filter. In the example corresponding to Figure 3.17, in which the reconstruction seems adequate, the Nyquist frequency $F_{s} ∕ 2$ is four times the signal BW. $□$

Combined digital filtering and D/S steps

When a digital filter $H_{z} (z)$ (subindices will be used here to avoid confusion and disambiguate $H (z)$ and $H (s)$ ) is part of an analog signal processing scheme such as the one depicted in Figure 3.16, it is sometimes useful to combine the roles of $H_{z} (z)$ and D/S into one “analog” filter with frequency response $H_{z} (e^{jω T_{s}})$ . This can be interpreted as a simple abscissa scaling in graphs such as Figure 3.15. Another view is that, while Eq. (3.24) refers to a sampled signal, a corresponding version of an equivalent (analog) “system” is

H_{s} (ω) = H_{z} (e^{j Ω}) |_{Ω = ω T_{s}} = H_{z} (e^{jω T_{s}}) .

(3.26)

³ It avoids the “ $sin (x) ∕ x$ ” distortion in frequency domain associated to a pulse train.

⁴ If needed, recall the notation for sampled signals in Section 1.7.1.

⁵ See, e. g., references in Appendix A.26.4.

⁶ For example, in [Lyo10].

⁷ Figure 3.17 and Figure 3.18 were generated with figs_systems_showDACFilterEffect.m, which uses both a low and high sampling frequencies to mimic the reconstruction via an analog filter.