Linear Time-Invariant Systems

3.4 Linear Time-Invariant Systems

This section is dedicated to the study of linear and time-invariant (LTI) systems.

Figure 3.5: Diagram of systems, emphasizing the linear and time-invariant (LTI) systems and the systems described by linear, constant-coefficient differential (or difference) equations (LCCDE).

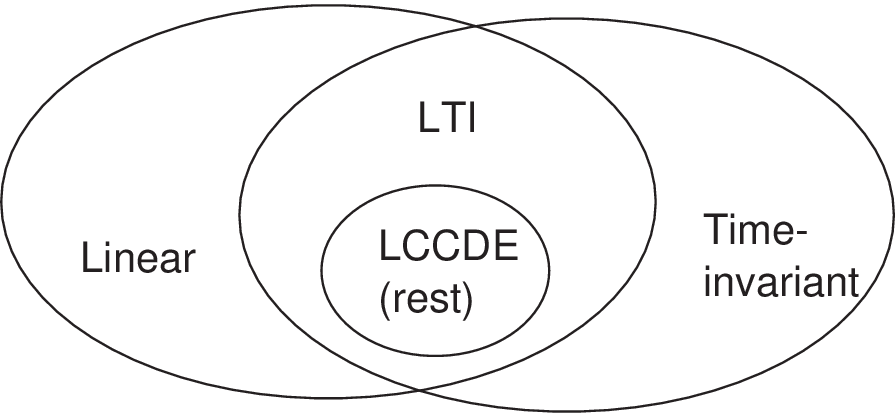
Figure 3.5 depicts the position of LTI systems and also includes the important subset of systems described by linear, constant-coefficient differential (or difference, in discrete-time) equations (LCCDE). In this text, it is assumed that the LCCDE systems have zero initial conditions or, equivalently, that the system is at rest.

3.4.1 Impulse response and convolution for LTI systems

A LTI system is completely characterized by its impulse response.¹ This fact is illustrated in the sequel using a simple example. Assume that a system $H$ is LTI and its impulse response $h [n] = 2 δ [n] + 5 δ [n - 1]$ is obtained by imposing an input $x [n] = δ [n]$ . For example, assuming $x [n] = 4 δ [n] - 3 δ [n - 1]$ , one has

\begin{array}{l} y [n] & = H {x [n]} = H {4 δ [n] - 3 δ [n - 1]} \\ = 4 H {δ [n]} - 3 H {δ [n - 1]} & (using linearity) \\ = 4 h [n] - 3 h [n - 1] & (using time-invariance) \\ = 4 (2 δ [n] + 5 δ [n - 1]) - 3 (2 δ [n - 1] + 5 δ [n - 2]) \\ = 8 δ [n] + 14 δ [n - 1]) - 15 δ [n - 2] . \end{array}

This example illustrates that, knowing $h [n]$ and using linearity and time-invariance, one can calculate the output.

In general, the input/output relation of a LTI depends on two facts:

As indicated by Eq. (1.3), any signal can be decomposed as the sum of impulses $αδ [n - n_{0}]$ that are shifted in time (by $n_{0}$ ) and scaled (by $α$ ) in amplitude.
By time-invariance, each impulse $δ [n - n_{0}]$ generates a sequence $h [n - n_{0}]$ at the output and by linearity these sequences $αh [n - n_{0}]$ can be scaled and summed to composed the output $y [n]$ .

These two key facts lead to the convolution operation:

\begin{align} y [n] & = H {x [n]} = H {\sum_{k = - \infty}^{\infty} x [k] δ [n - k]} \\ = \sum_{k = - \infty}^{\infty} x [k] H {δ [n - k]} & (using linearity) \\ = \sum_{k = - \infty}^{\infty} x [k] h [n - k] (using time-invariance) & (3.1) \end{align}

Note how linearity and time-invariance were both invoked in this proof. The continuous-time convolution is similar:

y (t) = \int_{- \infty}^{\infty} x (τ) h (t - τ) dτ .

(3.2)

The convolution is so important that it is represented by the operator $*$ . For example, $y [n] = x [n] * h [n]$ denotes the convolution of $x [n]$ and $h [n]$ . Because $*$ is the same symbol used for multiplication in programming languages, the context has to distinguish them.

Figure 3.6: Example of convolution between $x [n] = 2 δ [n] - 3 δ [n - 1]$ and $h [n] = δ [n] - 2 δ [n - 1] + δ [n - 2]$ . The top-left and top-right plots are $x [n]$ and $y [n]$ , respectively, while the other plots are the parcels of $x [n]$ (left) and the corresponding parcels of $y [n]$ (right).

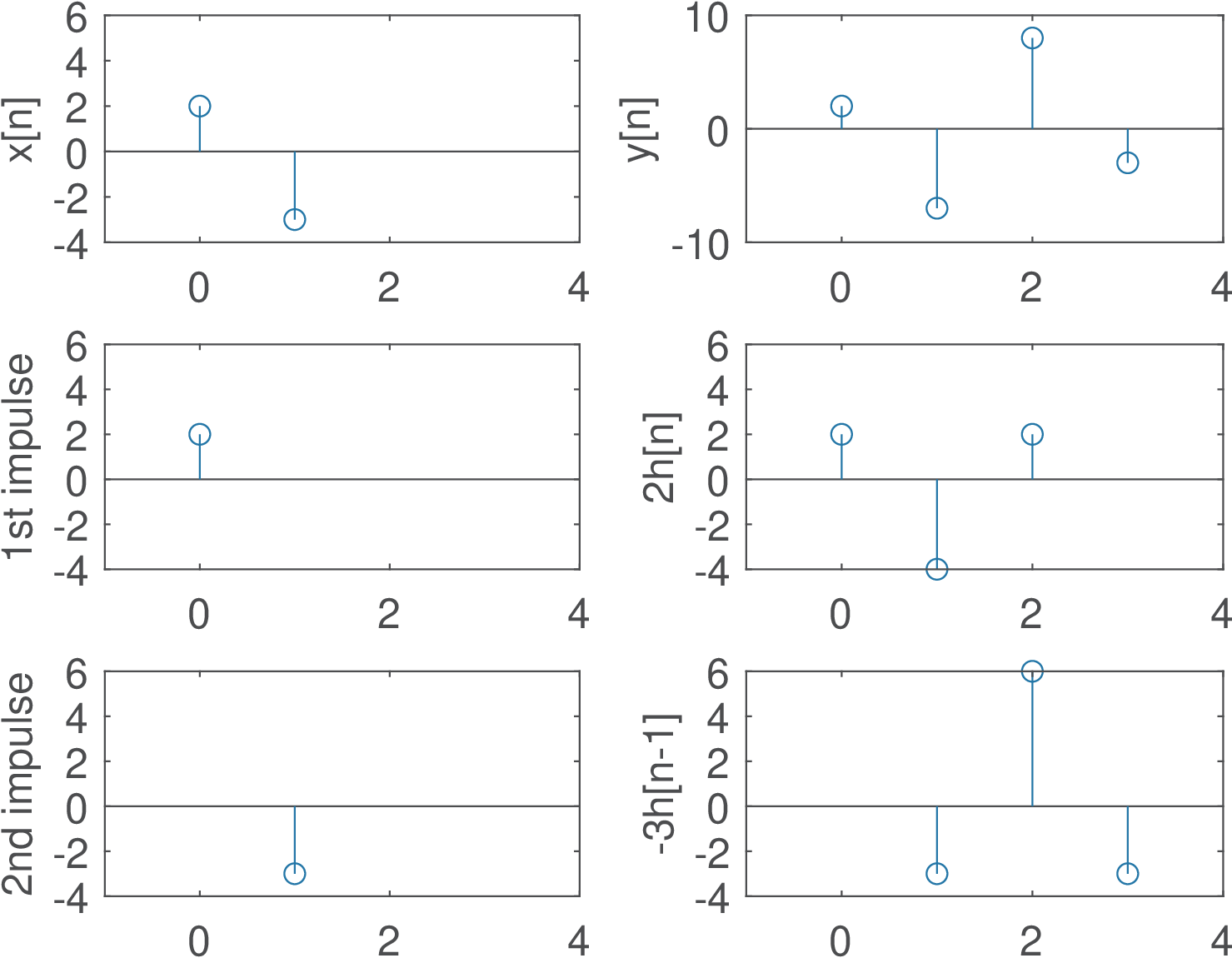
Figure 3.6 illustrates the convolution between two sequences. The interpretation is that $y [n]$ is composed by the sum of several scaled and shifted impulse responses. The plots at the right in Figure 3.6 indicate that $y [n]$ is the sum of the two parcels $2 h [n]$ and $- 3 h [n - 1]$ . The Listing 3.1 provides an example of implementing convolution of discrete-time sequences,² which gives the same result as the (faster) conv function in Matlab/Octave.

Listing 3.1: MatlabOctaveFunctions/ak_convolution.m

1function y=ak_convolution(x,h) 
2% function y=ak_convolution(x,h) 
3%convolution between sequences x and h 
4N1=length(x); %get the number of samples in x 
5N2=length(h); 
6N=N1+N2-1; %this is the number of samples in the output y 
7y=zeros(1,N); %pre-allocate space for y[n] 
8for i=1:N1 %calculate y[n]= sum_k x[k] h[n-k] 
9    y(i:i+N2-1)=y(i:i+N2-1)+x(i)*h; %scaling h by x(i) 
10end

Note that if the samples of $x [n]$ and $h [n]$ are organized as elements of vectors of polynomial coefficients, convolving them is equivalent to multiplying the two polynomials. For the example in Figure 3.6 one can obtain the convolution result by multiplying the equivalent polynomials $2 x - 3$ and $x^{2} - 2 x + 1$ , which leads to $2 x^{3} - 7 x^{2} + 8 x - 3$ , i. e., the coefficients are the samples of $y [n]$ .

If the impulse response completely characterizes a LTI system, all its properties can be inferred from the corresponding impulse response. This is discussed in Appendix A.27.7.

3.4.2 Advanced: Convolution properties

The convolution is:

Commutative: $a * b = b * a$
Associative: $a * (b * c) = (a * b) * c$
Distributive: $a * (b + c) = a * b + a * c$

Some other facts about the convolution:

If $N_{1}$ and $N_{2}$ are the duration in samples of two finite-length discrete-time sequences $a$ and $b$ , then $a * b$ has duration $N_{1} + N_{2} - 1$ samples
The expression Eq. (1.51) can also be written as $R_{X} (τ) = x (τ) * x^{*} (- τ)$
If $a [n] = b [n] * c [n]$ , to obtain $a [n_{a}]$ for a specific instant $n_{a}$ , one sums all products $b [n_{b}] c [n_{c}]$ for $n_{a} = n_{b} + n_{c}$

An example of this last fact is appropriate: if $x 1 [n] = δ [n] + 2 δ [n - 1] + 3 δ [n - 2]$ and $x 2 [n] = 5 δ [n] + 6 δ [n - 1] + 7 δ [n - 2] + 8 δ [n - 3]$ , the output $y [n] = x 1 [n] * x 2 [n]$ is given by

y[0] = x1[0] x2[0] = 5
y[1] = x1[0] x2[1] + x1[1] x2[0] = 16
y[2] = x1[0] x2[2] + x1[1] x2[1] + x1[2] x2[0] = 34
y[3] = x1[0] x2[3] + x1[1] x2[2] + x1[2] x2[1] = 40
y[4] = x1[1] x2[3] + x1[2] x2[2] = 37
y[5] = x1[2] x2[3] = 24

where one can note that the indexes of the input sequences sum up to the index of the output. Hence, one can alternatively implement convolution as in Listing 3.2.

Listing 3.2: MatlabOctaveFunctions/ak_convolution2.m

1function [y,n]=ak_convolution2(x1,x2,n1,n2) 
2% function [y,n]=ak_convolution2(x1,x2,n1,n2) 
3%calculate the convolution between the sequences x1 and x2 
4%that start at index n1 and n2, respectively 
5%Example: [y,n]=ak_convolution2(1:3,5:8,-3,2); stem(n,y) 
6N1=length(x1); %get the number of samples in x1 
7N2=length(x2); %get the number of samples in x2 
8N=N1+N2-1; %this is the number of samples in the output y 
9y=zeros(1,N); %pre-allocate space for y[n] 
10for i=0:N1-1 %calculate y[n] = sum_k x1[k] x2[n-k] 
11    for j=0:N2-1 
12        y(i+j+1) = y(i+j+1) + x1(i+1)*x2(j+1); %update 
13    end 
14end 
15n=n1+n2:n1+n2+N-1; %generate the "time" indices

Note that Listing 3.2 allows to explicitly deal with sequences that do not start at $n = 0$ . When using Matlab/Octave, it is often necessary to explicitly deal with and generate the time indexes.

It can be observed from Listing 3.2 that the first non-zero sample of the convolution between two sequences $x_{1} [n]$ and $x_{2} [n]$ is located at $n = n_{1} + n_{2}$ , which are assumed to be the indexes of the first non-zero samples of the two sequences. Similarly, the last non-zero sample of the convolution is the sum of the indexes of the last non-zero samples of $x_{1} [n]$ and $x_{2} [n]$ . This can be seen by running Listing 3.3.

Listing 3.3: MatlabOctaveCodeSnippets/snip_systems_ak_convolution.m. [ Python version]

1x1=1:3; %define sequence x1 
2x2=5:8; %define sequence x2 
3nx1=-3:-1; %define abscissa for x1 
4nx2=2:5; %define abscissa for x2 
5subplot(311); stem(nx1,x1) 
6subplot(312); stem(nx2,x2) 
7[y,n]=ak_convolution2(x1,x2,-3,2); %calculate convolution 
8subplot(313); stem(n,y) %show result with proper time axis

3.4.3 Advanced: Convolution via correlation and vice-versa

Given that convolution and cross-correlation are tightly related, Listing 3.4 illustrates how the Matlab/Octave functions xcorr and conv can be used to calculate the other operation.

Listing 3.4: MatlabOctaveCodeSnippets/snip_systems_convolution_correlation.m. [ Python version]

1x=(1:4)+j*(4:-1:1); %define some complex signals as row vectors, such 
2y=rand(1,15)+j*rand(1,15); %that fliplr inverts the ordering 
3%% Correlation via convolution 
4Rref=xcorr(x,y); %reference of a cross-correlation 
5xcorrViaConv=conv(x,conj(fliplr(y))); %use the second argument 
6%% Convolution via correlation 
7Cref=conv(x,y); %reference of a convolution 
8convViaXcorr=xcorr(x,conj(fliplr(y))); %using the second argument 
9%convViaXcorr=conj(fliplr(xcorr(conj(fliplr(x)),y))); %alternative 
10%% Make sure they have the same length and compare the results 
11if length(x) ~= length(y) %this case requires post-processing because 
12    %xcorr assumes the sequences have the same length and uses 
13    %zero-padding if they do not. We treat the effect of these zeros: 
14    convolutionLength=length(x)+length(y)-1; 
15    correlationLength=2*max(length(x),length(y))-1; 
16    if length(x) < length(y) %zeros at the end 
17        convViaXcorr = convViaXcorr(1:convolutionLength); 
18        xcorrViaConv = [xcorrViaConv zeros(1,correlationLength- ... 
19            length(xcorrViaConv))]; 
20    elseif length(x) > length(y) %zeros at the beginning 
21        convViaXcorr = convViaXcorr(end-convolutionLength+1:end); 
22        xcorrViaConv = [zeros(1,correlationLength- ... 
23            length(xcorrViaConv)) xcorrViaConv]; 
24    end 
25end 
26ErroXcorr= max(abs(Rref - xcorrViaConv)) %calculate maximum errors 
27ErroConv = max(abs(Cref - convViaXcorr)) %should be small numbers

As indicated in Listing 3.4, the key step to mimic a convolution via correlation or vice-versa is to flip the signal using $x (- t)$ , use its complex conjugate and eventually shift by $t_{0}$ as indicated in

\hat{x} (t) = x^{*} (- t + t_{0}) .

(3.3)

3.4.4 Advanced: Discrete-time convolution in matrix notation

Convolution can be denoted in matrix notation. This is especially convenient when dealing with finite-duration discrete-time signals. When these signals are represented by column vectors $x_{1}$ and $x_{2}$ , a convolution matrix $H_{1}$ allows to obtain the convolution result $y = x_{1} * x_{2}$ as

y = H_{1} x_{2},

(3.4)

where $H_{1}$ is composed by the elements of $x_{1}$ . It is also possible to create $H_{2}$ from the elements of $x_{2}$ and use $y = H_{2} x_{1}$ .

This can be better understood with examples. Considering the goal is to obtain the convolution of two column vectors x1=[1; 2; 3] and x2=[5; 6; 7; 8] (previous example), instead of using y=conv(x1,x2), one can create a matrix

hmatrix = [
     1     0     0     0
     2     1     0     0
     3     2     1     0
     0     3     2     1
     0     0     3     2
     0     0     0     3]

with the command hmatrix = convmtx(x1,length(x2)), and then calculate the convolution with y=hmatrix * x2. Note that when using row vectors, the commands could be hm = convmtx(x1,length(x2)); x2*hm (in this case, hm would be the transpose of hmatrix). Application 3.8 discusses the issue of repeatedly processing blocks of samples using the convolution in matrix notation. The matrices created by convmtx are Toeplitz matrices and the command toeplitz.m can also be useful to compose convolution matrices.

3.4.5 Approximating continuous-time via discrete-time convolution

Some situations require approximating the continuous-time convolution denoted by Eq. (3.2) via the discrete-time convolution in Eq. (3.1). In such cases, the sampling interval $T_{s}$ should be used as a normalization factor, as indicated in Eq. (A.31). This factor is adopted in the next example.

Example 3.2. Convolution of a pulse with itself leads to a triangular waveform. Assume a pulse $p (t) = 4 rect (5 t - 0.1)$ (see $rect (\cdot)$ in Section 1.3.6) with amplitude $A = 4$ V and support $T_{0} = 0.2$ s. The convolution $p (t) * p (t)$ corresponds to a triangular waveform: it is 0 for $t < 0$ and assumes its maximum value at $A^{2} T_{0} = 4^{2} \times 0.2 = 3.2$ at 0.2 s, which corresponds to the time that the two pulses overlap completely and $A^{2} T_{0}$ is the area of $p^{2} (t)$ . Figure 3.7 depicts both the pulse and continuous-time convolution $p (t) * p (t)$ .

Figure 3.7: Convolution of a pulse $p (t) = 4 rect (5 t - 0.1)$ with itself, obtained with Listing 3.5.

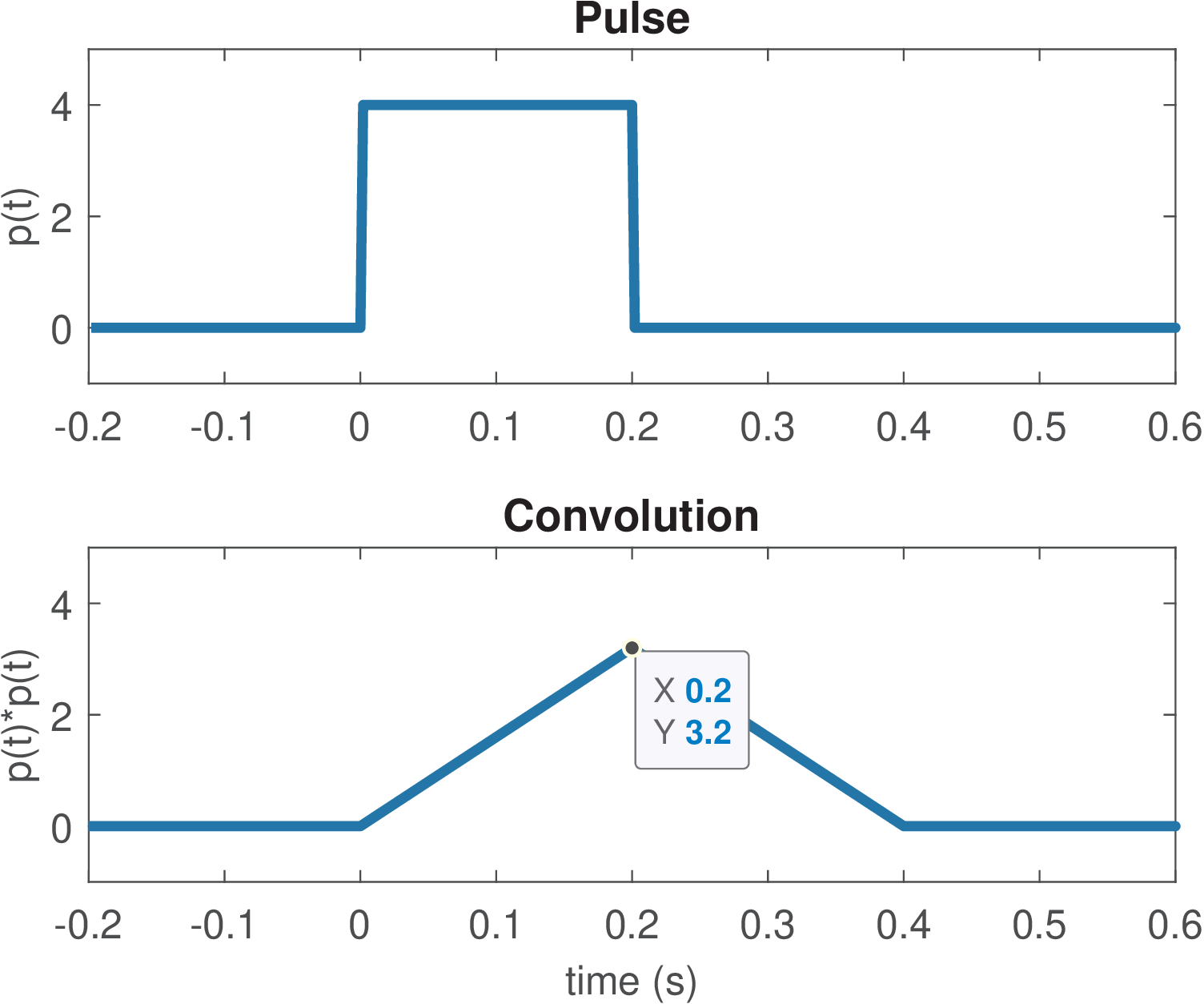
But Figure 3.7 was in fact obtained by representing $p (t)$ via its discrete-time version $p [n]$ , and approximating the convolution $p (t) * p (t)$ with the scaled discrete-time convolution $T_{s} (p [n] * p [n])$ , i. e., Eq. (A.31). Listing 3.5 shows the first lines of the script that generated Figure 3.7. After running Listing 3.5, the vectors pulse and triangle are shown in Figure 3.7 with the proper time axes.

Listing 3.5: MatlabOctaveCodeSnippets/snip_systems_continuous_discrete_conv

1T0=0.2; %pulse "duty cycle" (interval with non-zero amplitude): 0.2 s 
2Ts=2e-3; %sampling interval: 2 ms 
3N=T0/Ts; %number of samples to represent the pulse "duty cycle" 
4A=4; %pulse amplitude: 4 Volts 
5pulse=A*[zeros(1,N) ones(1,N) zeros(1,4*N)]; %pulse 
6triangle=Ts*conv(pulse,pulse); %(approximated) continuous convolution 
7disp(['Convolution peak at ' num2str(T0) ' is ' num2str(A^2*T0)])

Note in line 6 the scaling factor $T_{s}$ , which leads to the correct values, as indicated by the datatip in Figure 3.7. $□$

3.4.6 Frequency response: Fourier transform of the impulse response

As indicated in Table 3.1, the frequency response of an LTI system is the Fourier transform of its impulse response. In continuous-time it will be denoted by $H (f)$ ( $f$ in Hz) or $H (ω)$ ( $ω$ in rad/s), while in discrete-time the notation is $H (e^{j Ω})$ ( $Ω$ in rad). The frequency response is particularly useful because complex exponentials are eigenfunctions of LTI systems as explained in the sequel.

Eigenfunctions

Eigenfunctions are closely related to eigenvectors. if $A$ is a matrix (a linear transformation), a non-null vector $x$ is an eigenvector of $A$ if there is a scalar $λ$ such that

A x = λ x .

The scalar $λ$ is an eigenvalue of $A$ corresponding to the eigenvector $x$ . In general, the matrix $A$ generates a completely new vector $y = A x$ , i. e., $y$ and $x$ have different directions and magnitudes. However, if $x$ is an eigenvector of $A$ , then $y = λ x$ , which means that the operation changed only the magnitude of $x$ , leaving its direction unchanged (or possibly reversing it in case $λ < 0$ ).

Similarly, for any LTI system $H$ (continuous-time is assumed here), a complex exponential is an eigenfunction because the output is $y (t) = λ e^{j ω_{0} t}$ when the input is $x (t) = e^{j ω_{0} t}$ . The frequency response is useful because the eigenvalue $λ = H (ω_{0})$ is the value of the frequency response $H (ω)$ at the specific frequency $ω = ω_{0}$ . This implies that an LTI never creates new frequencies, because it can simply change the magnitude and phase of frequencies that were presented at its input. This fact can be represented as

e^{j ω_{0} t} \to H \to H (ω_{0}) e^{j ω_{0} t} .

It is then possible to analyze an LTI in the frequency domain by following the steps:

f 1.: Decompose the input as a sum (if the signal is periodic) or integral of complex exponentials. For that, one can use the Fourier series or transform $X (ω) = F {x (t)}$
f 2.: Obtain the frequency response, which provides the eigenvalues for all frequencies: $H (ω) = F {h (t)}$
f 3.: Conceptually, multiply each complex exponential $e^{j ω_{0} t}$ by its eigenvalue $H (ω_{0})$ and add the partial results to obtain the system output $y (t)$ . In practice, this step is performed by $Y (ω) = H (ω) X (ω)$ and then using the inverse transform to obtain $y (t) = F^{- 1} {Y (ω)}$ .

Figure 3.8: Frequency response of $H (ω) = \frac{1}{jω + 2}$ represented in polar form: magnitude (top) and phase (bottom). The data tips indicate the values for $ω = \pm 4$ rad/s.

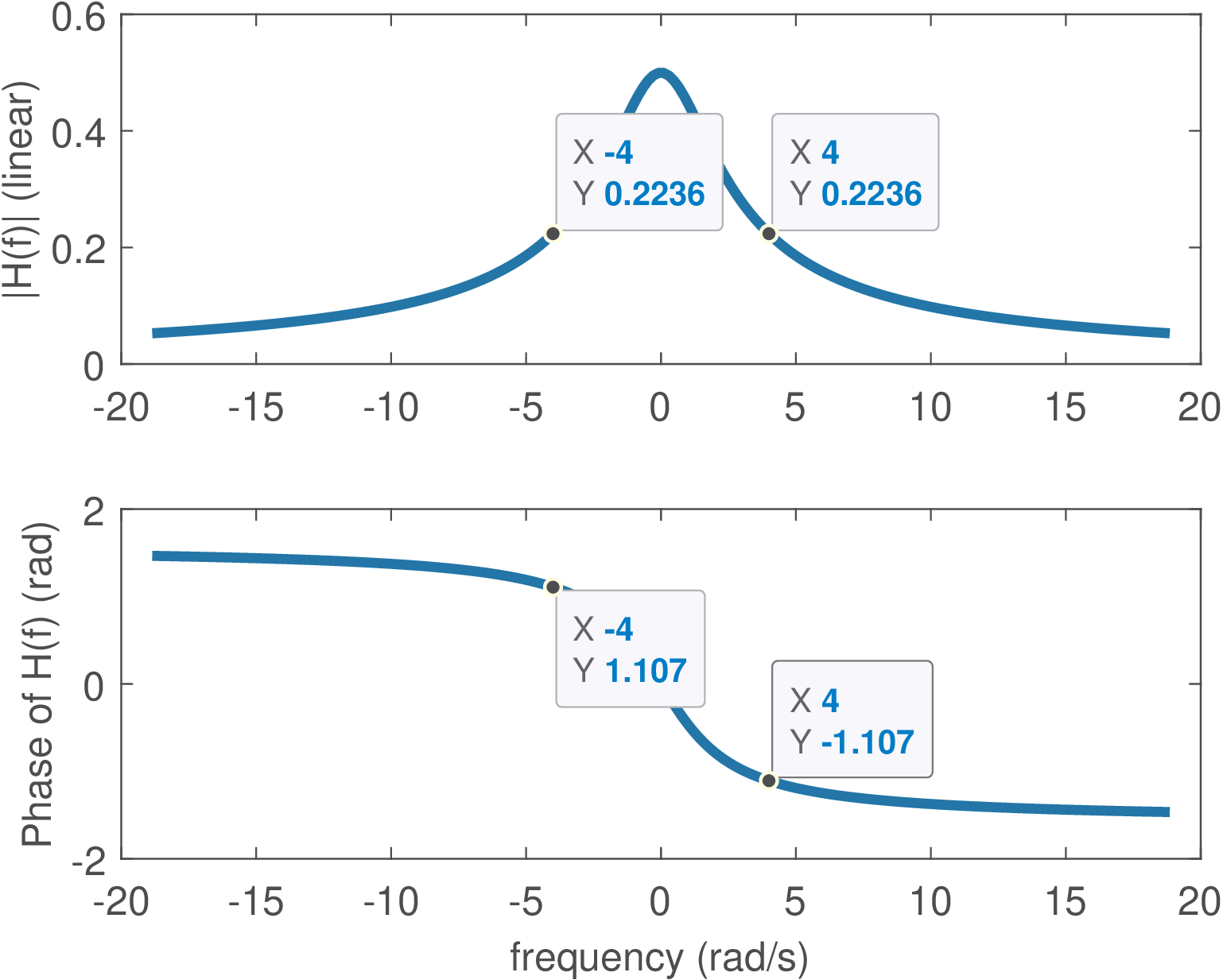
Example 3.3. LTI filtering of continuous-time complex exponential. For example, consider that $x (t) = 6 e^{j 4 t} + 6 e^{- j 4 t} = 12 cos (4 t)$ is the input of an LTI with $h (t) = e^{- 2 t} u (t)$ . The eigenvalues corresponding to each the complex exponential eigenfunctions with frequencies $ω = \pm 4$ rad/s can be obtained from the frequency response $H (ω) = F {h (t)} = \frac{1}{jω + 2}$ . The Matlab/Octave commands Omega=4; H=1/(j*Omega+2) calculate $H (ω) |_{ω = 4} = 0.1 - 0.2 j$ for the positive frequency. Because $h (t)$ is real-valued, the frequency response presents Hermitian symmetry and $H (ω) |_{ω = - 4} = H^{*} (ω) |_{ω = 4}$ , i. e., $H (ω) |_{ω = - 4} = 0.1 + 0.2 j$ . The commands abs(H), angle(H) can transform from Cartesian to polar: $H (ω) |_{ω = 4} \approx 0.2236 e^{- j 1.107}$ and $H (ω) |_{ω = - 4} \approx 0.2236 e^{j 1.107}$ . Therefore, the output is $y (t) = (0.2236 e^{- j 1.107}) 6 e^{j 4 t} + (0.2236 e^{j 1.107}) 6 e^{- j 4 t} = 1.32 e^{j (4 t - 1.11)} + 1.32 e^{j (- 4 t + 1.11)} = 2.64 cos (4 t - 1.11)$ .

The effect of the LTI system was to impose a gain of $| H (4) | = 0.2236$ and a phase of $∠H (4) = - 1.107$ rad. Figure 3.8 depicts the frequency response for a range $ω = 2 π [- 3, 3]$ rad/s. Because of the Hermitian symmetry (when $h (t)$ is real), it is common to plot only the positive frequencies. For example, investigate the command freqs(1,[1 2]), which shows the frequency response of $H (ω) = \frac{1}{jω + 2}$ in a different format. $□$

The previous discussion was restricted to exponentials of the form $e^{j ω_{0} t}$ , but a general complex exponential $e^{st}$ (with $σ \neq 0$ ) is also an eigenfunction of any LTI and the eigenvalue is given by the Laplace transform $H (s)$ , as represented by

e^{s_{0} t} \to H \to H (s_{0}) e^{s_{0} t} .

The frequency response $H (e^{j Ω})$ of discrete-time LTI systems is also very useful. When the time axis $t$ is discretized by sampling, i. e., $t = n T_{s}$ , the complex exponential $e^{st}$ becomes $e^{sn T_{s}}$ , which is more conveniently represented by $z^{n}$ , where

z = e^{s T_{s}}

with $z, s \in ℂ$ .

The discrete-time complex exponential $z^{n}$ is an eigenfunction of discrete-time LTI systems. To prove that, consider $x [n] = {(z_{0})}^{n}, z_{0} \in ℂ$ , then

\begin{array}{l} y [n] & = \sum_{k = - \infty}^{\infty} {(z_{0})}^{k} h [n - k] = ∑_{k = - \infty}^{\infty} h [k] {(z_{0})}^{n - k} = {(z_{0})}^{n} ∑_{k = - \infty}^{\infty} h [k] {(z_{0})}^{- k} \\ = {(z_{0})}^{n} H (z) |_{z = z_{0}} . \end{array}

The eigenvalue $H (z) |_{z = z_{0}}$ can be obtained from the transfer function

H (z) = \sum_{n = - \infty}^{\infty} h [n] z^{- n},

which is the Z-transform of the system’s impulse response. As a special case, when $| z | = 1$ , the eigenfunction $e^{j Ω n}$ has its amplitude and phase eventually modified by a LTI as depicted by:

e^{j Ω_{0} n} \to H \to H (e^{j Ω_{0}}) e^{j Ω_{0} n} .

Example 3.4. LTI filtering of discrete-time complex exponentials. This example describes how an LTI system filters a complex exponential. Consider that $x [n] = 4 e^{j 0.5 πn} + 4 e^{- j 0.5 πn} = 8 cos (0.5 πn)$ is the input of an LTI with $h [n] = 0 . 7^{n} u [n]$ . The eigenvalues can be obtained from $H (e^{j Ω}) = F {h [n]} = \frac{1}{1 - 0.7 e^{- j Ω}}$ when $Ω = 0.5 π$ rad. The Matlab/Octave commands omega=pi/2; H=1/(1-0.7*exp(-j*omega)) calculate $H (e^{j Ω}) |_{Ω = 0.5 π} = 0.6711 - 0.4698 j$ . Because $h [n]$ is real-valued, the frequency response presents Hermitian symmetry. The commands abs(H), angle(H) can transform from Cartesian to polar: $H (e^{j Ω}) |_{Ω = 0.5 π} \approx 0.8192 e^{- j 0.6107}$ . Therefore, the output is $y [n] = (0.8192 e^{- j 0.6107}) 4 e^{j 0.5 πn} + (0.8192 e^{j 0.6107}) 4 e^{- j 0.5 πn} = 3.2769 e^{j (0.5 πn - 0.6107)} + 3.2769 e^{j (- 0.5 πn + 0.6107)} = 6.5539 cos (0.5 πn - 0.6107)$ . The effect of the LTI system was to impose a gain of $0.8192$ and a phase of $- 0.6107$ rad.

Figure 3.9: Frequency response of $H (e^{j Ω}) = \frac{1}{1 - 0.7 e^{- j Ω}}$ represented in polar form: magnitude (top) and phase (bottom). The data tips indicate the values for $Ω = π ∕ 2$ rad.

Figure 3.10: Version of Figure 3.9 obtained with the command freqz(1,[1 -0.7]).

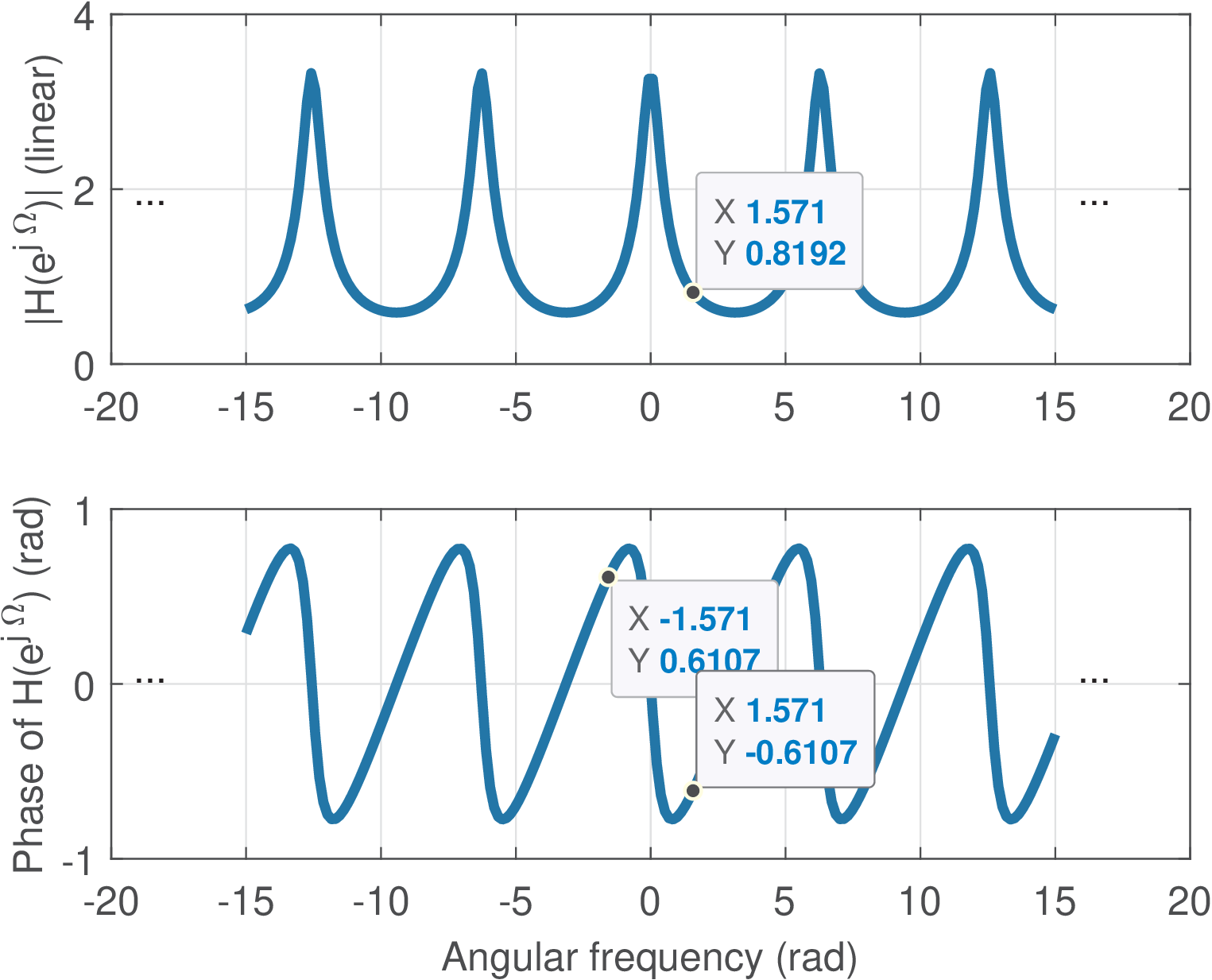
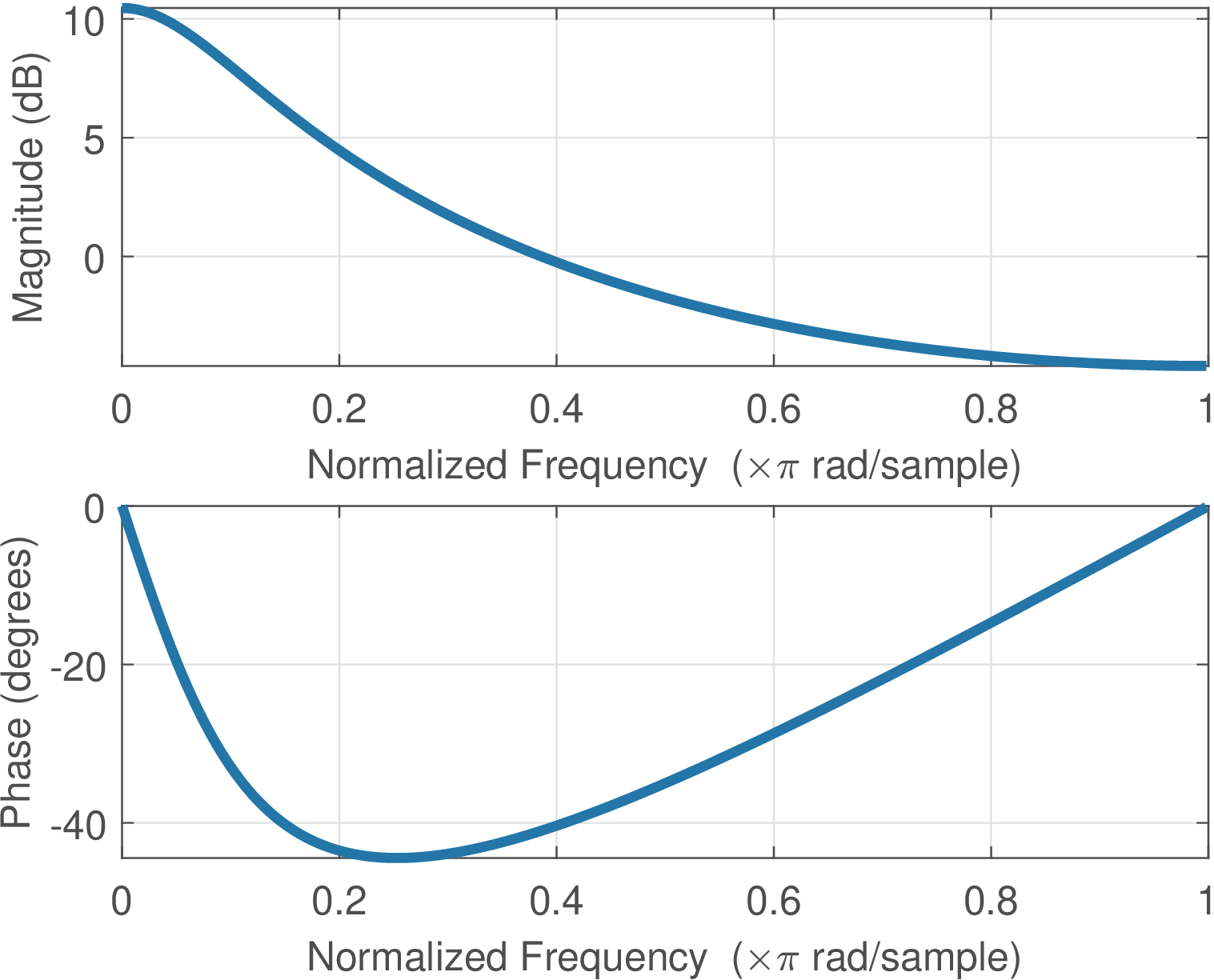
Figure 3.9 depicts the frequency response for a range $Ω = [- 15, 15]$ rad. As expected, $H (e^{j Ω})$ is periodic because $H (e^{j Ω}) = H (e^{j (Ω + 2 π)})$ . Given this periodicity and the Hermitian symmetry (when $h [n]$ is real), it is common to plot only the positive frequencies in the range $Ω = [0, π]$ . For example, Figure 3.10 shows the plots obtained with the command freqz(1,[1 -0.7]), which shows the frequency response of $H (e^{j Ω})$ with the magnitude in dB, the phase in degrees (instead of rad) and the abscissa in a “normalized frequency” $Ω ∕ π$ that maps $[0, π]$ into $[0, 1]$ . $□$

3.4.7 Fourier convolution property

The convolution property of Fourier transforms states that the convolution between two signals has a Fourier transform given by the multiplication of their Fourier transforms. In other words, the convolution between these signals by can be obtained as the inverse Fourier transform of the multiplication of their Fourier transforms. For example, assuming continuous-time, the convolution $y (t) = x_{1} (t) * x_{2} (t)$ can be obtained with

y (t) = F^{- 1} {X_{1} (f) X_{2} (f)},

(3.5)

where $X_{1} (f)$ and $X_{2} (f)$ are the corresponding Fourier transforms. Similarly, in discrete-time, the convolution result $y [n]$ can be written as

y [n] = x_{1} [n] * x_{2} [n] = {DTFT}^{- 1} {X_{1} (e^{j Ω}) X_{2} (e^{j Ω})},

(3.6)

where $X_{1} (e^{j Ω})$ and $X_{2} (e^{j Ω})$ are the corresponding DTFTs and, in this case, $F^{- 1}$ denotes the inverse DTFT.

Example 3.5. Convolution using DTFTs and inverse DTFT. For example, if $x_{1} [n] = α_{1}^{n} u [n]$ and $x_{2} [n] = α_{2}^{n} u [n]$ are two discrete-time complex exponentials with $| α_{1} | < 1$ and $| α_{2} | < 1$ , their DTFTs are $X_{i} (e^{j Ω}) = 1 - α_{i} e^{- j Ω}, i = 1, 2$ , respectively. The convolution result is

y [n] = x_{1} [n] * x_{2} [n] = \frac{1}{α_{1} - α_{2}} (α_{1}^{n + 1} u [n] - α_{2}^{n + 1} u [n])

(3.7)

and can be obtained via the inverse DTFT of $Y (e^{j Ω})$ , which is given by

Y (e^{j Ω}) = X_{1} (e^{j Ω}) X_{2} (e^{j Ω}) = \frac{1}{(1 - α_{1} e^{- j Ω}) (1 - α_{2} e^{- j Ω})} .

(3.8)

Eq. (3.7) can be obtained by using partial fraction expansion of Eq. (3.8). $□$

Due to the duality of Fourier transforms, the multiplication in time-domain corresponds to convolution in frequency-domain between the respective spectra. This is called the multiplication property and corresponds to

x_{1} (t) x_{2} (t) \Leftrightarrow X_{1} (f) * X_{2} (f) = \int_{- \infty}^{\infty} X_{1} (p) X_{2} (f - p) d p .

(3.9)

in continuous-time.

In discrete-time, one needs to take in account that the spectra are periodic and the conventional convolution is not adequate when both signals are periodic. In fact, the multiplication property for discrete-time signals is

x_{1} [n] x_{2} [n] \Leftrightarrow \frac{1}{2 π} \int_{< 2 π >} X (e^{j Ω}) X_{2} (e^{j (Ω - 𝜃)}) d𝜃 .

(3.10)

The integral in Eq. (3.10) differs from a conventional convolution because it is calculated over only one period ( $2 π$ rad in this case) and the result is normalized by this period. This modified convolution is denoted as $⊛$ and is called periodic, cyclic or circular convolution. As in a Fourier series expansion to obtain coefficients $c_{k}$ , the associated period must be known in order to properly use $⊛$ . The normalization by the period can be incorporated in its definition, which leads to the following expression for the periodic convolution:

x_{1} (t) ⊛ x_{2} (t) = \frac{1}{T} \int_{< T >} x_{1} (τ) x_{2} (t - τ) d τ,

(3.11)

where both signals are periodic in $T$ .

The definition of Eq. (3.11) allows to write Eq. (3.10) as

x_{1} [n] x_{2} [n] \Leftrightarrow X (e^{j Ω}) ⊛ X_{2} (e^{j Ω}),

(3.12)

where the period $2 π$ is implicit.

The periodic convolution corresponds to performing the conventional convolution (called “linear” convolution, in contrast to “circular”) between $x_{1} (t)$ and $x'_{2} (t)$ , where $x'_{2} (t)$ is a single period of $x_{2} (t)$ that is normalized by the period $T$ . The interval to define $x'_{2} (t)$ can be conveniently chosen as $x_{2}^{'} (t) = x_{2} (t) ∕ T, 0 \leq t < T$ , or $0$ otherwise, or $x_{2}^{'} (t) = x_{2} (t) ∕ T, - T ∕ 2 \leq t < T ∕ 2$ , or $0$ otherwise.

As discussed in the sequel, the periodic convolution is typically associated to FFT-based processing.

3.4.8 Circular and fast convolutions using FFT

Recalling that the FFT corresponds to sampling the DTFT, Eq. (3.6) suggests that FFTs can be used to efficiently compute a convolution. However, even if $x [n]$ were not periodic, when its DTFT $X (e^{j Ω})$ is sampled (in frequency domain) by the FFT, the FFT values $X [k]$ are representing the spectrum of a periodic version of $x [n]$ . Consequently, when FFTs substitute DTFTs in Eq. (3.6), the result is not the linear but the circular convolution represented as

y [n] = x_{1} [n] ⊛ x_{2} [n] = {FFT}^{- 1} {X_{1} [k] X_{2} [k]},

(3.13)

where both FFTs must have the same length $N$ , which plays the whole of the period of a circular convolution.

Listing 3.6 provides an example of using Eq. (3.13). Note how zero-padding is used to assure the element-wise multiplication fft(x,N).*fft(h,N) uses arrays with the same length. The result of Listing 3.6 confirms that, in general, linear and circular convolution differ.

Listing 3.6: MatlabOctaveCodeSnippets/snip_systems_circularConvolution.m. [ Python version]

1x=[1 2 3 4]; h=[.9 .8]; %signals to be convolved 
2shouldMakeEquivalent=0 %in general, linear and circular conv. differ 
3if shouldMakeEquivalent==1 
4    N=length(x)+length(h)-1; %to force linear and circular coincide 
5else 
6    N=max(length(x),length(h)); %required for FFT zero-padding 
7end 
8linearConv=conv(x,h) %linear convolution 
9circularConv=ifft(fft(x,N).*fft(h,N)) %circular convolution, N=4 
10%circularConv=cconv(x,h,N) %note that Matlab has the cconv function

If the value of shouldMakeEquivalent is made equal to 1, Listing 3.6 returns the same results for both linear and circular convolutions. In fact, when the FFT length is at least the number of non-zero samples of the convolution output, the circular and linear convolution results coincide. This suggests that Eq. (3.13) can be used to calculate a linear convolution, provided that the FFT length is made long enough.

Obtaining a linear convolution via FFTs is trickier when one of the signals to be convolved has infinite duration. In this case, it is obviously not possible to find a large enough FFT length to use Eq. (3.13). However, if the other signal has finite duration, it is feasible and often used in practice to segment the long signal into blocks and calculate the linear convolution by sequentially calculating one FFT per block and properly combining the results. There are basically two alternatives to combine the intermediate results that are called overlap-add and overlap-save methods, and are roughly equivalent. Listing 3.7 illustrates the former.

Listing 3.7: MatlabOctaveCodeSnippets/snip_systems_overlapAdd.m. [ Python version]

1x=1:1000; %infinite duration (or "long") input signal 
2h=ones(1,3); %non-zero samples of finite-length impulse response 
3Nh=length(h); %number of impulse response non-zero samples 
4Nb=5; %block (segment) length 
5Nfft=2^nextpow2(Nh+Nb-1); %choose a power of 2 FFT size 
6Nx = length(x); %number of input samples 
7H = fft(h,Nfft); %pre-compute impulse response DFT, with zero-padding 
8beginIndex = 1; %initialize index for first sample of current block 
9y = zeros(1,Nh+Nx-1); %pre-allocate space for convolution output 
10while beginIndex <= Nx %loop over all blocks 
11    endSample = min(beginIndex+Nb-1,Nx);%last sample of current block 
12    Xblock = fft(x(beginIndex:endSample),Nfft); %DFT of block 
13    yblock = ifft(Xblock.*H,Nfft); %get circular convolution result 
14    outputIndex  = min(beginIndex+Nfft-1,Nh+Nx-1); %auxiliary variab. 
15    y(beginIndex:outputIndex) = y(beginIndex:outputIndex) + ... 
16        yblock(1:outputIndex-beginIndex+1); %add parcial result 
17    beginIndex = beginIndex+Nb; %shift begin of block 
18end 
19stem(y-conv(x,h)) %compare the error with result from conv

A typical application of the overlap-add and overlap-save methods is to compute the output of a LTI system represented by a finite-duration impulse response (i. e., a FIR filter, as will be discussed in Section 3.14). Listing 3.7 provides an example where the impulse response has only three non-zero samples, and the long input signal is segmented in blocks of Nb=5 samples.

¹ Say you meet a person that tells you he/she is a LTI system. You should then ask his/her impulse response. If you know it, just relax because you can perfectly calculate the person’s reaction (output) to any situation (input).

² On the Web one can find applets instructing about continuous and discrete convolution (see, e. g., [ url3jhu]).