Exercises

3.20 Exercises

3.1. When the input $x_{1} [n] = δ [n] + δ [n - 1]$ is applied to a linear system, the observed output is $y_{1} [n] = 4 δ [n - 1] + δ [n - 2]$ . Inform the expression of the output $y_{2} [n]$ when the input is $x_{2} [n] = 3 δ [n] + 3 δ [n - 1]$ .
3.2. When the input $x_{1} [n] = δ [n]$ is applied to a LTI system, the output is $y_{1} [n] = 3 δ [n] + 2 δ [n - 1] + δ [n - 2]$ . What is the output $y_{2} [n]$ when the input is $x_{2} [n] = 5 δ [n] + 2 δ [n - 1]$ ?
3.3. When the input $x_{1} [n] = δ [n]$ is applied to a system, the output is $y_{1} [n] = 3 δ [n] + 2 δ [n - 1] + δ [n - 2]$ , and when the input is $x_{2} [n] = 2 δ [n - 1]$ , the output is $y_{2} [n] = 6 δ [n - 1] + 2 δ [n - 2] + 2 δ [n - 3]$ . Can this system be LTI?
3.4. A time-invariant system has output $y_{1} (t) = δ (t - 1) - δ (t - 4)$ when the input is $x_{1} (t) = δ (t)$ . Inform the expression of the output $y_{2} (t)$ when the input is $x_{2} (t) = δ (t - 3)$ .
3.5. The input-output relations that describe three given systems are: 1) $y [n] = C {(x [n])}^{2}$ , where $C = 2 e^{jπ ∕ 2}$ , 2) $y [n] = (n - 1) x [n]$ and 3) $y [n] = 3 x [n - 1] + 2^{π} x [n - 3]$ . Classify whether or not these systems are: a) causal, b) linear, c) memoryless, d) stable in BIBO sense and e) time-invariant.
3.6. A discrete-time LTI is characterized by the difference equation $y [n + 2] = 5 x [n + 2] + 2 x [n + n_{0}]$ , where $x [n]$ and $y [n]$ are the input and output signals, respectively. Inform a value for $n_{0}$ that makes the system causal.
3.7. What is the convolution matrix $H$ for an impulse response $h [n] = 3 δ [n] + 2 δ [n - 1] + δ [n - 2]$ when the input signals are: a) column vectors of dimension 3, b) row vectors of dimension 4?
3.8. Four continuous-time signals: $x_{1} (t) = e^{j 4 t}$ , $x_{2} (t) = e^{- j 4 t}$ , $x_{3} (t) = cos (4 t)$ and $x_{4} (t) = e^{(- 1 + j 4) t}$ , are individually transmitted over a causal system $H (s) = \frac{1}{s + 10}$ . What are the respective outputs $y_{1} (t), \dots, y_{4} (t)$ ?
3.9. Four discrete-time signals: $x_{1} [n] = 5 e^{j 2 n}$ , $x_{2} [n] = e^{- j 2 n}$ , $x_{3} [n] = cos (2 n)$ and $x_{4} [n] = {(3 e^{j 2})}^{n}$ , are individually transmitted over the causal system $H (z) = \frac{1}{1 - 0.6 z^{- 1}}$ . What are the respective outputs $y_{1} [n], \dots, y_{4} [n]$ ?
3.10. What is the result of the periodic convolution between a pulse train $x (t)$ with pulses with duty cycle of 2 s, amplitude of 5 V and a period of 10 s with itself? Assume $x (t)$ is an even signal.
3.11. The following commands were used to calculate y1 and y2:

1N=3;M=4;x=1:M;h=[0.4,-0.1];y1=conv(x,h);y2=ifft(fft(x,N).*fft(h,N));

a) What is the minimum value of N to make y1 and y2 coincide? b) Generalize the previous answer for an arbitrary value of M and length(h).
3.12. A band-limited signal $x (t)$ was sampled obeying the sampling theorem with $F_{s} = 10$ Hz and the result is $x_{s} (t) = 4 δ (t) + 3 δ (t - 0.1) - 2 δ (t - 0.4)$ . Provide the exact expression of $x (t)$ . Hint: this expression is given in terms of scaled and shifted sincs.
3.13. An AM radio signal $x (t)$ has a bandwidth of 10 kHz at baseband and is centered at $f_{c} = 600$ MHz (the passband signal occupies 20 kHz). Use undersampling to obtain a discrete-time baseband version $x_{b} [n]$ of this signal via digital signal processing based on a signal $x [n]$ obtained with the minimum sampling frequency that you think is possible assuming realistic (non-ideal) filters. Describe the whole scheme informing the adopted: a) analog anti-aliasing filter, b) sampling frequency, c) any required digital filtering and/or frequency digital down-conversion, and d) phase inversion compensation (in case the signal replica at positive frequency $f_{c}$ was moved to a lower frequency than the replica at $- f_{c}$ ).
3.14. A band-limited even and real-valued discrete-time signal $x [n]$ has the spectrum $X (e^{j Ω})$ described in Figure 3.86 with $Ω_{1} = π ∕ 4$ and $Ω_{2} = π ∕ 2$ rad. It is converted to a continuous-time signal $x (t)$ using the scheme depicted in Block (3.25) with $F_{s} = 1$ kHz and a ZOH modeled by $h (t) = u (t) - u (t - T_{s})$ . a) Carefully draw $| X (f) |$ , where $X (f) = F {x (t)}$ in the range $- 3$ to 3 kHz. b) Calculate $X (f)$ (magnitude and phase) at $f = 0, 100$ and 1200 Hz. c) Repeat the calculation in b) but now considering that $x [n]$ is a critically sampled signal with $Ω_{1} = π ∕ 4$ but $Ω_{2} = π$ rad.

Figure 3.86: Spectrum of a band-limited even and real-valued signal $x [n]$ .

3.15. Assume the DUT in the circuit of Figure A.34 is the SAW filter described in Table 3.4 (assume its typical parameters). Both the source

Z_{S}

and load

Z_{L}

impedances are 100

Ω

. a) If the input signal

x (t)

(denoted as

V_{s}

in Figure A.34) is a sinusoid of frequency 70 MHz and power 4 dBm, what is the power over the load and a reasonable expression for the output signal

y (t)

? b) If

x (t) = 3 cos (ω_{1} t) + 6 cos (ω_{2} t)

with

ω_{1} = 2 π \times 70

and

ω_{2} = 2 π \times 76.5

Mrad/s, what is a reasonable expression for the output

y (t)

?
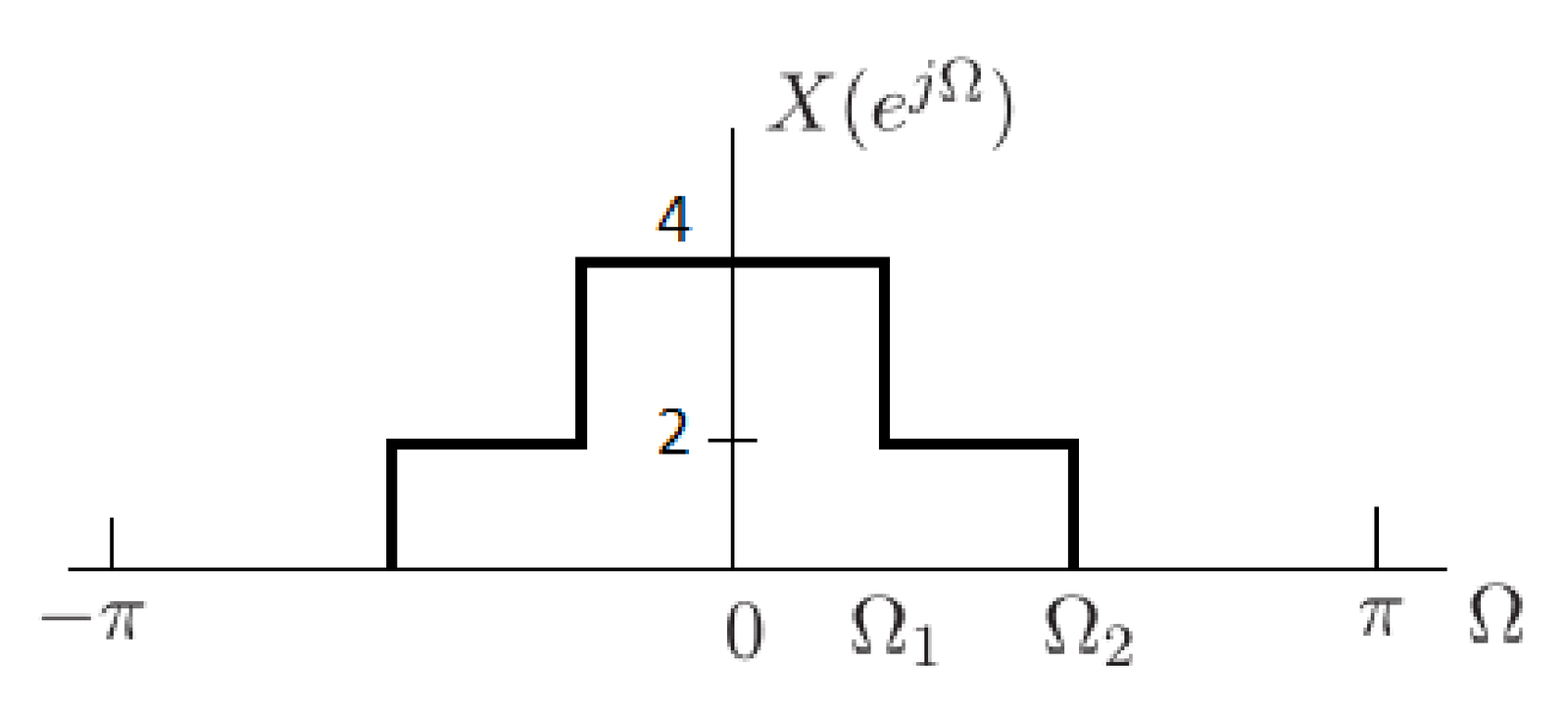
3.16. If the input to the filter characterized by Table 3.5 is

x (t) = 4 cos (2 π f_{1} t + π ∕ 4) + 8 cos (2 π f_{2} t)

, where

f_{1} = 455

and

f_{2} = 500

kHz, what is a reasonable expression for the output

y (t)

?
3.17. A non-causal analog lowpass filter has an ideal magnitude with unitary gain for frequencies

- 5

to 5 rad/s and zero otherwise. The phase of this filter is linear and given by

e^{- j 8 ω}

. What is the output of this filter when the input is

x (t) = \sum_{k = 0}^{\infty} 0 . 5^{k} sin (1.5 kt)

?
3.18. A FIR filter with linear phase has an impulse response

h [n] = 3 δ [n] - 5 δ [n - 1] + 7 δ [n - 2] - 5 δ [n - 3] + 3 δ [n - 4]

. Find its system function

H (z)

and draw a realization of this filter with the minimum number of multipliers.
3.19. a) Design two filters

H_{1} (s)

and

H_{2} (s)

, both described by

(ω_{n}^{2}) ∕ (s^{2} + 2 ζ ω_{n} s + ω_{n}^{2})

, with damping factors

ζ = 0.707

and

0.9

, respectively. In the case of

H_{2} (s)

, assume a natural frequency

ω_{n} = 1600

rad/s and a tolerance

𝜖 = 0.05

. In both cases, the settling time must be approximately 3 ms. b) Plot and compare the graphs of the output waveforms of both systems to the step function

u (t)

.
3.20. For the filter

H (z)

obtained with [b, a]=butter(3,1/3): a) find the values of

H (z)

for

z = 0.5 + 0.5 j, 3 + 2 j, 0, - 1, 3

and

0.5 + 0.5 j

. b) Using freqz.m, find the maximum value of the magnitude response and in which frequency this maximum occurs. c) What are the first five samples of the impulse response

h [n]

? d) Is this a FIR or IIR? e) Is this a lowpass or highpass?
3.21. For the filter

H (s) = \frac{100}{s^{2} + 10 \sqrt{2} s + 100}

(obtained with [Bs,As]=butter(2,10,’s’)); a) what are the values in Hertz of its natural and cutoff frequencies? Now consider that

H (s)

is the anti-aliasing filter of a DSP system operating with a sampling frequency of

F_{s} = 4

Hz and there is a strong interferer tone with 1 dBm at 5 Hz that contaminates the signal before the filter

H (s)

. b) At what frequency and power this interferer will appear within the band

[0, F_{s} ∕ 2 [

? c) And what if the interferer has the same power of 1 dBm but frequency of 50 Hz?
3.22. a) Using syntax and structure similar to Listing 3.12, list the algorithm of a digital filter implementing the system function

H (z)

provided by [Bz,Az]=butter(3,0.2). b) When

H (z)

is used in the canonical system of Figure 3.30 with

F_{s} = 44.1

kHz and ideal analog filters, what is the corresponding cutoff frequency in Hertz of the overall system?
3.23. The filter

H (s) = \frac{1}{s^{3} + 2 s^{2} + 2 s + 1}

was obtained with the command [b, a]=butter(3,1,’s’) and has cutoff frequency of 1 rad/s. Obtain a filter

G (s)

that corresponds to a scaled version of

H (s)

with a new cutoff frequency of

1200 π

rad/s such that both have the same gain at DC. a) Inform the linear gains

| H (ω) |

and

| G (ω) |

for both filters at frequencies

ω = 0, 1, 1200 π

and 2000 rad/s. b) What are these gains in dB?
3.24. A filter

H (s) = \frac{125}{s^{3} + 10 s^{2} + 50 s + 125}

has a cutoff frequency of 5 rad/s. Obtain a filter

G (s)

that corresponds to a version of

H (s)

scaled in frequency with a cutoff frequency of 3 rad/s.

G (s)

should also have a gain of 3 dB at DC.
3.25. a) Use the six methods of Table 3.6 to convert

H (s) = 0.13 ∕ (s^{2} - 0.4 s + 0.13)

into

H (z)

assuming

T_{s} = 0.1

s and compare their frequency responses with the original one (in continuous-time) b) Repeat the procedure for

T_{s} = 1

s. c) Discuss what methods were most impacted by the increase of

T_{s}

.
3.26. Given a filter

H (s) = (0.1 s^{2} + 71) ∕ (s^{2} + 11 s + 71)

and assuming

F_{s} = 50

Hz, a) find

H (z)

using the bilinear transform, b) compare the frequency responses of

H (s)

and

H (z)

after D/C conversion using the same abscissa in rad/s, c) can you find a frequency

ω_{m} > 0

in rad/s for which the values of

H (s)

and

H (z)

are the same?
3.27. A filter

H (s) = (0.1 s^{2} + 71) ∕ (s^{2} + 11 s + 71)

should be converted to

H (z)

using the bilinear. The value of

H (s)

s_{1} = j 8.24

and

s_{2} = j 5

are

g_{1} \approx 0.708 e^{- j 1.5366}

and

g_{2} \approx 0.9554 e^{- j 0.8743}

, respectively. a) Find

H_{1} (z)

and

H_{2} (z)

that when implemented in a hardware using

F_{s} = 50

Hz leads to the same values

g_{1}

and

g_{2}

ω_{d} = 8.24

and 5 rad/s, respectively, which correspond to the frequencies

Ω = ω_{d} ∕ F_{s} = 0.1648

and 0.1 rad. b) For comparison, show the values of

H_{i} (e^{j 0.1648})

and

H_{i} (e^{j 0.1})

, for

i = 1

and 2. c) To note the degrees of freedom, use frequency scaling such that

G (s) |_{s = s_{2}} = H (s) |_{s = s_{1}} = g_{1}

and then find

G (z)

such that when implemented in a hardware using

F_{s} = 50

Hz leads to the same value

g_{1}

ω_{d} = 5

rad/s.
3.28. The filter

H_{s} (s) = (0.1 s^{2} + 71) ∕ (s^{2} + 11 s + 71)

should be converted to

H_{z} (z)

using the bilinear such that the value of

H_{s} (jω)

ω = 10

rad/s is the same value

H_{z} (e^{j Ω})

will have at

Ω = π ∕ 4

rad. a) find the value of

F_{s}

that allows to directly convert

H_{s} (s)

into

H_{z} (z)

without the traditional pre-warping step, b) assuming an arbitrary value of

F'_{s} = 0.5

Hz, find the pre-warped version of

H_{s} (s)

that will generate the correct

H_{z} (z)

via bilinear with

F'_{s}

.
3.29. A product adopted an analog filter

H (s) = \frac{125 \times 1 0^{6}}{s^{3} + 1 0^{3} s^{2} + 500 \times 1 0^{3} s + 125 \times 1 0^{6}}

, which was designed with [B,A]=butter(3,500,’s’) to have a cutoff frequency of 500 rad/s. This filter must be substituted by an equivalent system

H_{e} (s)

that relies on a digital filter

H (z)

. The anti-aliasing and reconstruction filters are ideal. The ADC and DAC converters should operate at

F_{s} = 800

Hz. Design a digital filter

H (z)

with the bilinear transform, such that

H_{e} (s)

has the same cutoff frequency of

H (s)

.
3.30. Design a causal FIR

H (z)

using the windowing method. The filter must have 5 coefficients, cutoff frequency

π ∕ 6

rad and the adopted window must be Hann’s. The gain at DC must be unitary. The command hanning(5) in Matlab/Octave, returns [0.25, 0.75, 1.00, 0.75, 0.25].
3.31. A filter was obtained with [b, a]=butter(3,1/3). a) Draw the block diagram representation for realizations using direct form I, direct form II, transposed direct form II, cascade of SOS and parallel using SOS. b) Using any programming language, implement the direct form II. Assume that there is a function called readAD() that reads a sample from the ADC and another writeDA() that writes a sample to the DAC, and that the processing loop is correctly invoked according to the chosen sampling frequency. In other words, complete the following code (this example is in C):

1main( ) { 
2  int x, y; 
3  ... 
4  while (1) { //eternal loop 
5    x = readAD( ); 
6    ... 
7    writeDA(y); 
8  } 
9  ... 
10}