3.17  Advanced: Multirate Processing

Many modern DSP systems adopt distinct sampling rates along the processing chain, using interpolators and decimators. Two basic blocks of these multirate processing systems are the upsampler and downsampler.

3.17.1  Upsampler and interpolator

The upsampler has an output $q[m]=x[m∕L]$ for any $m$ that is an integer multiple of $L$ and 0 otherwise. It is represented by

Note that distinct indexes $m$ and $n$ are used to emphasize the sampling rates are not the same.

The upsampling by $L$ is not a time-invariant operation (in spite of being linear), so the system is not LTI. When the input is a WSS process, the output process cannot be assumed WSS.

The Fourier transform of the upsampler output is given by:

which corresponds to scaling the abscissa $\mathrm{\Omega }$ by the factor $L$ such that $Q(e^{j\mathrm{\Omega }})$ is a compressed version³⁹ of $X(e^{j\mathrm{\Omega }})$.

Figure 3.66 provides an example where the original spectrum $X(e^{j\mathrm{\Omega }})$ is an ideal lowpass filter with cutoff frequency ${\mathrm{\Omega }}_c=\pi ∕4$ rad. After upsampling by $L=4$, the resulting $Q(e^{j\mathrm{\Omega }})$ has not a lowpass spectrum anymore. In fact, the new “high frequency” components in $Q(e^{j\mathrm{\Omega }})$ are required to enable the amplitudes of the upsampler output $q[m]$ to vary from/to zero between two original samples of the (relatively “smooth”) input $x[n]$.

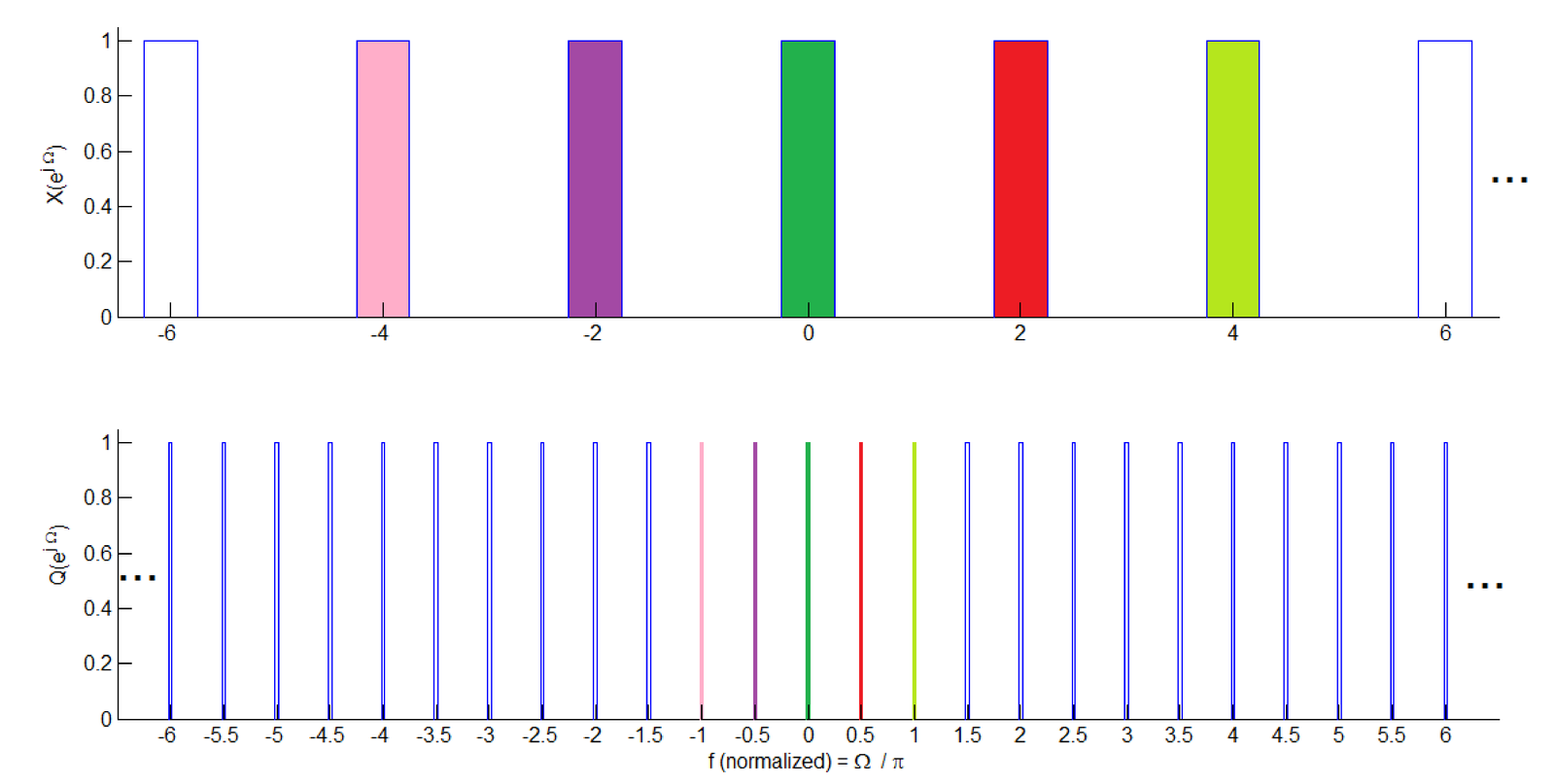
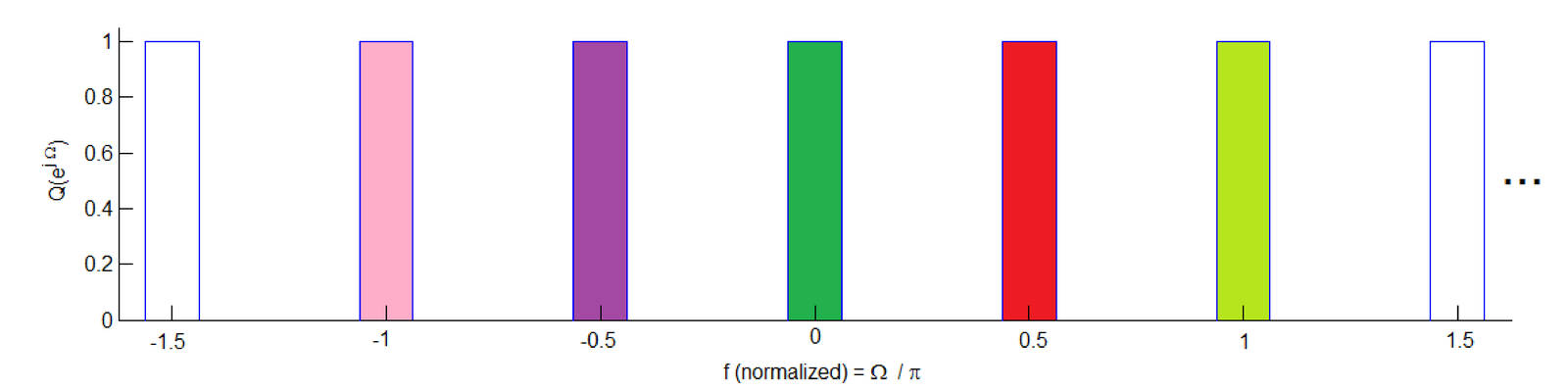
Notice that there is no aliasing or change in spectrum amplitude involved in this process, but within $[-\pi ,\pi [$ rad, $Q(e^{j\mathrm{\Omega }})$ has $L$ versions of what was the original $X(e^{j\mathrm{\Omega }})$ in the range $[-\pi ,\pi [$ rad as emphasized in Figure 3.67. In this example, with $L=4$, the equivalent of four replicas of the original spectrum can be found within $[-\pi ,\pi [$ rad: the ones centered at $f=-0.5,0,0.5$ and half of the replicas in $f=-1$ and 1.

The autocorrelations $R_x[l∕L]$ and $R_q[l]$ of the signals at, respectively, the input and output of an upsampler are related by

Assuming the entire bandwidth of the input is of interest, in order to eliminate all images within the interval $[-\pi ,\pi [$ except the one centered at $\mathrm{\Omega }=0$ (DC), a lowpass filter $H_i(z)$ should have a stopband starting at $\pi ∕L$. Otherwise, imaging will occur. Hence, an interpolator is composed of an upsampler and a lowpass filter, which is represented by

3.17.2  Downsampler and decimator

Meanwhile, the downsampler can be represented by

and has an output $y[n]=z[\mathit{nM}]$. Its spectrum can be expressed as:

In other words, the spectrum $Y(e^{j\mathrm{\Omega }})$ of the downsampled signal is the sum of $M$ stretched versions of the spectrum $Z(e^{j\mathrm{\Omega }})$ of the input signal $z[m]$.

As discussed in Example 1.5, the transformation $(\mathrm{\Omega }-2\mathit{\pi k})∕M$ of the independent variable $\mathrm{\Omega }$ corresponds to stretching the frequency axis by $M$ and shifting this intermediate result by $2\mathit{\pi k}$ rad. As indicated in Eq. (3.100), these $M$ individual versions are summed and the result is scaled by $1∕M$.

Figure 3.68 illustrates an example in which the original spectrum $Z(e^{j\mathrm{\Omega }})$ is downsampled by $M=3$. As indicated by Eq. (3.100), $Y(e^{j\mathrm{\Omega }})$ is composed by $M=3$ parcels and each one represented by one color in Figure 3.68.

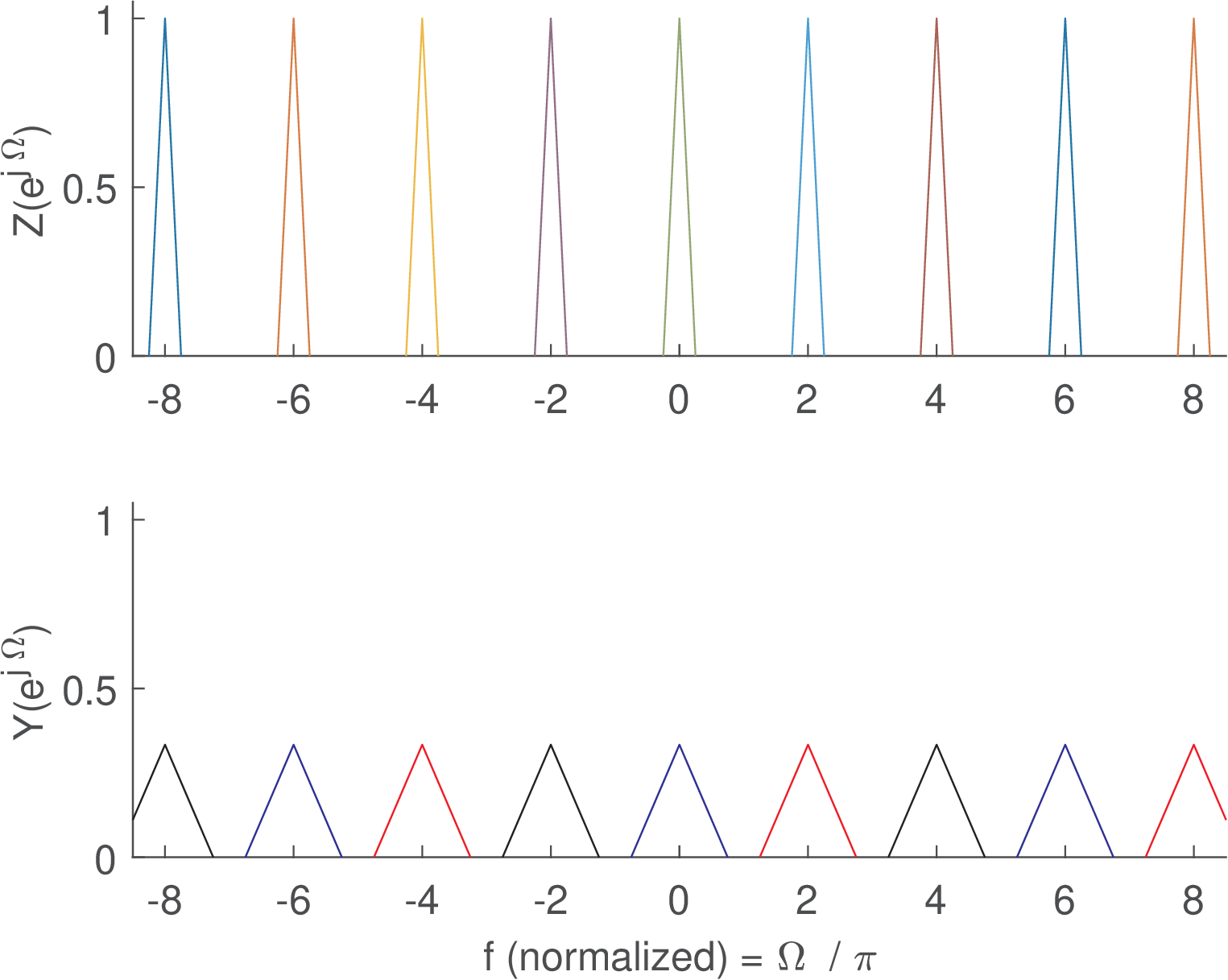
If one considers a single parcel $Z(e^{j(\mathrm{\Omega }-2\mathit{\pi k})∕M})$, it can be observed that a parcel itself is not periodic in $\mathrm{\Omega }=2\pi$, as required for any discrete-time signal spectrum. For example, $Z(e^{j\mathrm{\Omega }∕3})$(in blue) alone does not have a period of $2\pi$. The replica at $\mathrm{\Omega }=2\pi$ rad of the original spectrum is shifted to $M\times 2\pi =6\pi$ in $Y(e^{j\mathrm{\Omega }})$ and, consequently, $Z(e^{j\mathrm{\Omega }∕3})$ does not have a replica at $2\pi$ nor $4\pi$, but only at $\mathrm{\Omega }=6\pi$ and multiples. But when the parcel $Z(e^{j\mathrm{\Omega }∕3})$ is combined with $Z(e^{j(\mathrm{\Omega }-2\pi )∕3})$ (in red) and $Z(e^{j(\mathrm{\Omega }-4\pi )∕3})$ (in black), the resulting spectrum indeed indicates that $Z(e^{j\mathrm{\Omega }})$ has a period of $2\pi$.

Since the maximum frequency that can be represented after downsampling is reduced by a factor of $M$, any frequency beyond $\pi ∕M$ in the input will be aliased into the central period of the downsampled signal, as indicated by the $M-1$ replicas in Eq. (3.100). Hence, a decimator is composed of an anti-alising filter $H_d(z)$ designed with stopband edge at $\pi ∕M$ and a downsampler, as illustrated in

Note that an interpolator uses a lowpass filter after the upsampling operation to combat imaging, while a decimator uses the lowpass filter before downsampling in order to control aliasing.