A.26  Discrete and Continuous-Time Impulses

A.26.1  Discrete-time impulse function

The discrete-time impulse function $\delta [n]$, also called unit impulse and Kronecker’s delta, is a sequence that has amplitude equals to one at $n=0$ and zero otherwise. When $\delta [n]$ is multiplied by another (arbitrary) sequence $x[n]$, the result $y[n]=x[n]\delta [n]$ can be denoted by $y[n]=x[0]\delta [n]$, indicating that $x[0]$ is the only non-zero value of the new sequence. Hence, $\delta [n]$ allows to analyze (or “sift”) $x[n]$ when $n=0$. Delaying the impulse by $n_0$ samples (the amplitude is one only at $n=n_0$ now) and multiplying by $x[n]$, one obtains

The capability of “sifting”²³ a signal $x[n]$ using impulses is very useful as discussed in Section 1.3.4. The continuous-time version $\delta (t)$ of $\delta [n]$ is discussed in the sequel. Many properties are shared by $\delta (t)$ and $\delta [n]$, but $\delta (t)$ is more mathematically involved.

A.26.2  Why defining the continuous-time impulse? Some motivation

Before describing its mathematical properties, some motivation for using continuous-time impulses, also called Dirac’s delta, is presented.

A good motivation for the impulse $\delta (t)$ is the representational power of impulses in “density functions”. In many situations it is useful to represent properties of discrete variables using densities. For example, how could one represent the discrete random variable (r. v.) corresponding to the result of a dice roll as a continuous r.v. $Z$ and use a probability density function (PDF) instead of a probability mass function (PMF)? An impulse is capable of representing some “mass probability” in a PDF! Figure A.35 indicates the handy representation provided by impulses with areas equal to $1∕6$.

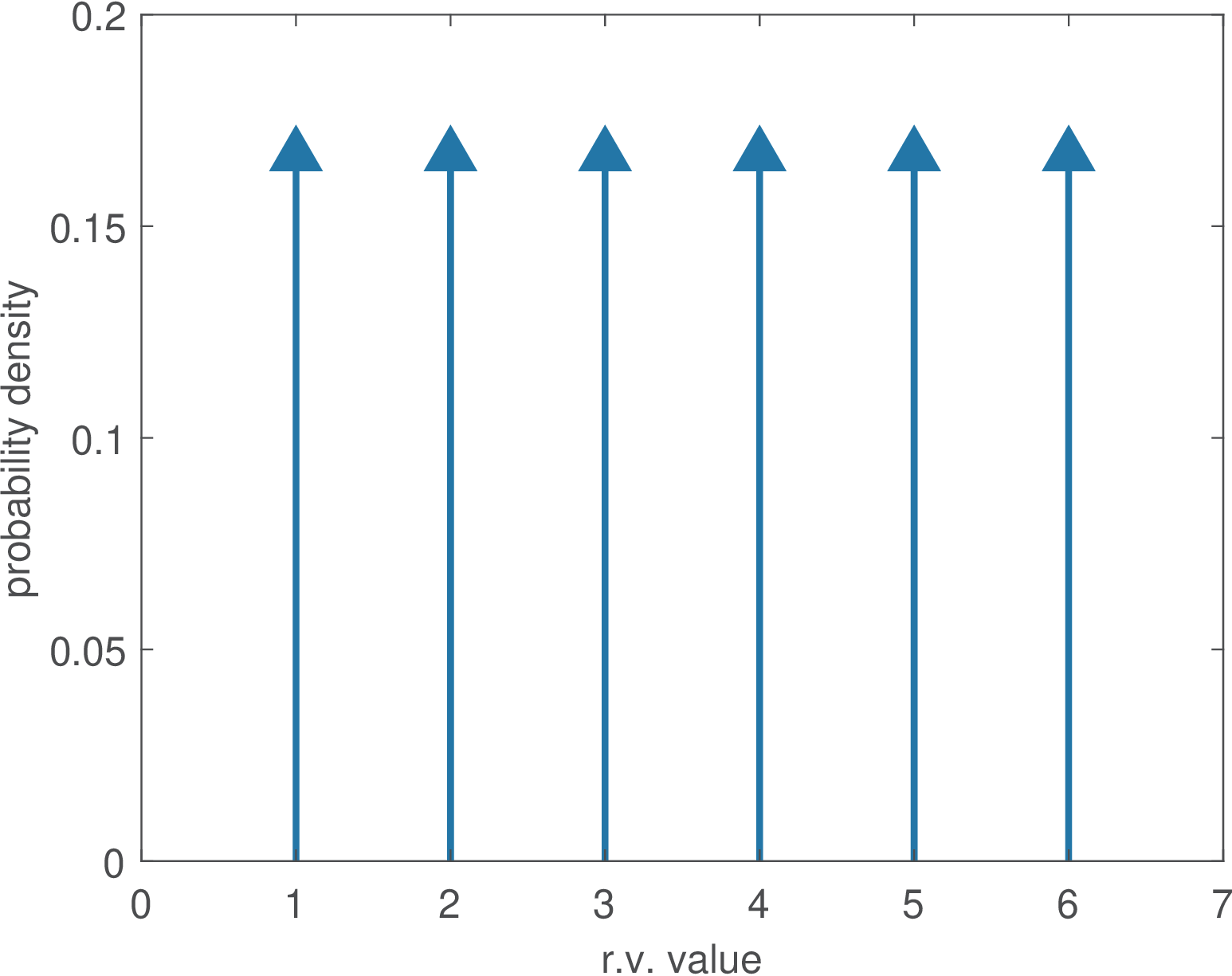
For illustrative purposes, it is common to plot an impulse with the arrow length proportional to its area as in Figure A.35, but one should not take the area as the amplitude value. The amplitude is not defined because it goes to infinite.

A.26.3  Definition of the continuous-time impulse as a limit

The impulse $\delta (t)$ can be obtained by considering a pulse $p(t)$ of duration $\mathrm{\Delta }$ and amplitude $1∕\mathrm{\Delta }$:

Note that the area of $p(t)$ is always 1 and, as $\mathrm{\Delta }$ goes to 0, its amplitude goes to $\infty$. It is also possible to obtain $\delta (t)$ as the limit of other functions, such as a Gaussian (see, e.g., [ urlBMimp]).

A.26.4  Continuous-time impulse is a distribution, not a function

It is tricky to deal with continuous-time impulses because they are not functions [Can21], but generalized functions [ urlBMdis].

Impulses can be manipulated via linear operations such as derivative and integral, but nonlinear operations or transformations such as $\text{log}<!--\; FUNCTION\; APPLICATION\; -->(\delta (t))$ and ${\delta }^2(t)$ cannot be defined to have the usual properties and require specific algebras such as Colombeau’s [ urlBMcol].

While $\delta (t)$ is not a function, in some signal processing tasks it may be manipulated as such. In contrast, the discrete-time impulse $\delta [n]$ has no mathematical difficulties in its definition or manipulation. It is a regular sequence that has all 0 amplitude for all values of $n$ but $n=0$, which has amplitude 1. In other words, while the amplitude of $\delta (t)$ is not defined (infinite), in discrete-time the amplitude is simply $\delta [0]=1$.

A.26.5  Mathematical properties of the continuous-time impulse

Sifting property

The sifting property of Eq. (A.120) also applies in continuous-time. This property states that multiplying $x(t)$ by a continuous-time impulse $\delta (t-t_0)$ results in $y(t)=x(t)\delta (t-t_0)=x(t_0)\delta (t-t_0)$ that is non-zero only at $t_0$ and $x(t_0)$ is the area of the impulse at $t_0$.

The sifting property is typically quoted as

when one wants to emphasize that $x(t_0)$ is a scalar and there is no more connection to time in this case. It is also possible to write

when one wants to emphasize that Eq. (A.122) can be repeatedly invoked, for all values of $t_0$ (represented as $t$ in this case) and recover the complete signal $x(t)$.

In most applications of the sifting property, the integral is not used and the property is quoted as

which can be interpreted as: when a function $x(t)$ is multiplied by an impulse at $t_0$, all values of $x(t)$ other than $x(t_0)$ become zero and non-relevant, such that the final result is a single impulse of area $x(t_0)$ located at $t_0$.

Scaling property

Assuming $a$ is a non-zero scalar, the scaling property of the impulse is

For example,

The scaling property is important to understand the different areas of impulses when using Hz or rad/s as the unit for frequency (the independent variable). For example, the Fourier transform of a cosine $x(t)=10\text{cos}<!--\; FUNCTION\; APPLICATION\; -->(6\mathit{\pi t})$ of frequency 3 Hz and amplitude 10 is represented by

or, equivalently,

The areas are different by a factor of $2\pi$ for $X(f)$ and $X(\omega )$ because $\omega =2\mathit{\pi f}$ and, by the scaling property, $\delta (\omega )=\delta (f)∕(2\pi )$. This can cause some confusion because when there are no impulses involved, it is trivial to convert a graph from $X(f)$ to $X(\omega )$ or vice-versa by scaling the abscissa (e. g., multiplying by $2\pi$ when converting from $f$ to $\omega$). However, all impulses should be scaled when the abscissa is modified.

A.26.6  Convolution with an impulse

When a signal $x(t)$ is convolved with an impulse $\mathit{a\delta }(t-t_0)$, the rule of thumb is to shift the origin of $x(t)$ to $t_0$ and scale it by the area $a$ of the impulse. Mathematically:

This is similar to $x[n]\ast \mathit{a\delta }[n-n_0]$ in discrete-time, but in discrete-time the scaling is by an amplitude $a$, not area.

A.26.7  Applications of the impulse

Complementing the example in Figure A.35, which used impulses to indicate mass probabilities represented as probability densities, one should notice that impulses are also used in “densities” when dealing with a Fourier transform $X(f)$. As indicated in Table 2.5, if $x(t)$ is in volts, $X(f)$ has units of volts/Hz. Hence, if $x(t)$ is periodic and has a representation as a Fourier series (analogous to a PMF), one can use impulses to represent the spectrum of $x(t)$ as a Fourier transform (analogous to using a PDF when the random variable is discrete and could be represented by a PMF).

Another example illustrates the importance of distinguishing the amplitude and area of a continuous-time impulse. As discussed in Section 1.10.1, the autocorrelation of a power signal at the origin is the average power. For AWGN with bilateral PSD $N_0∕2$, as indicated in Eq. (4.40), the power is infinite and its autocorrelation at the origin is an impulse with area $N_0∕2$. In other words, looking carelessly at the autocorrelation $R(\tau )=N_0∕2\delta (\tau )$ one could think that the average power is $N_0∕2$, but in fact $R(0)=\infty$.