Filtering Random Signals and the Impact on PSDs

4.5 Filtering Random Signals and the Impact on PSDs

This section investigates the result of processing a random input signal through a system, and how the output PSD relates to the input.

4.5.1 Response of LTI systems to random inputs

An important result of stochastic processes theory is that when the input of a LTI system is a WSS process $X (t)$ , the corresponding output is also a WSS process $Y (t)$ , as indicated below

X (t) \to h (t) \to Y (t),

where $h (t)$ is the impulse response of the LTI system.

Given that $H (f) = F {h (t)}$ is the frequency response of the system, the relationship between the PSDs $S_{y} (f)$ and $S_{x} (f)$ of $Y (t)$ and $X (t)$ , respectively, is given by

S_{y} (f) = | H (f) |^{2} S_{x} (f) .

(4.38)

Similarly, if a discrete-time WSS random process $X [n]$ is filtered by a LTI with impulse response $h [n]$ as in

X [n] \to h [n] \to Y [n],

the PSD of the WSS output process $Y [n]$ is given by

S_{y} (e^{j Ω}) = | H (e^{j Ω}) |^{2} S_{x} (e^{j Ω}),

(4.39)

where $H (e^{j Ω})$ is the DTFT of $h [n]$ .

4.5.2 Filtering continuous-time signals that have a white PSD

A signal model that is used in several applications is the white noise, previously discussed in Section 1.10.1.0. A realization $ν (t)$ of a continuous-time white noise process has autocorrelation

R (τ) = 𝔼 [ν (t) ν (t - τ)] = \frac{N_{0}}{2} δ (τ)

(4.40)

and zero mean $μ = 𝔼 [ν (t)] = 0$ .

Using Eq. (4.23), the bilateral PSD of a white noise is

S (f) = F {\frac{N_{0}}{2} δ (τ)} = \frac{N_{0}}{2}, \forall f .

(4.41)

When a unilateral representation is adopted, the white PSD is conveniently denoted as $S (f) = N_{0}$ . For instance, if $N_{0} = 6$ W/Hz is the constant level of a unilateral PSD, its bilateral representation has a constant level of $N_{0} ∕ 2 = 3$ W/Hz.

One can write $N_{0} ∕ 2$ or $N_{0}$ for the bilateral and unilateral PSDs, respectively, and in both cases the average power over a given frequency band⁸ $BW$ is

P = N_{0} BW

(4.42)

In other words, using this nomenclature, $P = N_{0} BW$ is valid for both unilateral and bilateral PSD representations, given that in the case of a bilateral PSD one needs to multiply the PSD level $N_{0} ∕ 2$ by $2 BW$ to find the average power $P$ .

Note from Eq. (4.40) and recalling Eq. (1.54) that the continuous-time white noise power has $R (0) = \infty$ because there is an impulse in $τ = 0$ (the area is $N_{0} ∕ 2$ but the amplitude goes to infinite). Another way of observing that the continuous time WGN has infinite power is looking at the frequency domain: its PSD is $S (f) = \frac{N_{0}}{2}$ , such that from Eq. (4.19), the area under the curve goes to infinite.

With infinite power, a white noise cannot be measured (it would damage the measuring equipment!). But white noise is a very good model for many practical applications, with an implicit assumption that limits the frequencies to some bandwidth of interest and makes measurements and simulations feasible. In other words, the noise can have a flat PSD only over a given finite bandwidth but, for the purpose of the experiment / simulation, be conveniently modeled as white noise.

Because power can be written as $P = σ^{2} + μ^{2}$ , and $μ = 0$ for a signal with a white spectrum, the continuous-time white noise variance $σ^{2} = P$ is infinite.

If the input $X (t)$ is white noise with autocorrelation $R (τ) = (N_{0} ∕ 2) δ (τ)$ and PSD $N_{0} ∕ 2$ , Eq. (4.38) informs that the PSD at the output of the LIT system is

S_{y} (f) = | H (f) |^{2} \frac{N_{0}}{2},

(4.43)

i. e., $S_{y} (f)$ is a scaled version of $| H (f) |^{2}$ .

All the previous discussion assumed the input signal has a white PSD. But the signal amplitudes could have any probability distribution, such as Laplacian, uniform, etc. A very special case of white noise is when this probability distribution is Gaussian, which corresponds to the so-called WGN, introduced earlier in Section 1.10.1.0.

4.5.3 Advanced: Filtering discrete-time signals that have a white PSD

It is important to distinguish the continuous-time white noise, which has a flat bilateral PSD with value $N_{0} ∕ 2$ watts/Hz and infinite power, from the discrete-time “white noise” that has finite power typically denoted by $σ^{2}$ . The discrete-time “white noise” is “white” (has a constant PSD level) only over the frequency band $[- F_{s} ∕ 2, F_{s} ∕ 2 [$ (but is still called “white”). To emphasize the similarities and differences between continuous and discrete-time white noise, the goals here are to discuss how to: 1) generate a discrete-time white noise, 2) interpret the conversion of a continuous-time white noise into a discrete-time version and 3) its conversion back to continuous-time.

Discrete-time white noise

As mentioned, a discrete-time white process $X [n]$ has its power $𝔼 [X^{2} [n]] = σ_{x}^{2}$ coinciding with the variance $σ_{x}^{2}$ because the mean $μ_{x}$ has to be zero for white processes. Moreover, its bilateral PSD level $S_{x} (e^{j Ω}) = σ_{x}^{2}$ coincides with its variance in watts. This PSD can be interpreted as $σ_{x}^{2} ∕ (2 π)$ watts per radians. To observe that, note from Eq. (4.21) that

P = \frac{1}{2 π} \int_{< 2 π >} S (e^{j Ω}) d Ω = \frac{σ^{2}}{2 π} \times 2 π = σ^{2} .

In other words, the constant PSD level $σ^{2}$ has the same numerical value of the power $σ^{2}$ in watts. In case of a unilateral PSD, the constant value $2 σ^{2}$ would be twice the power.

Therefore, a discrete-time bilateral white PSD (with a constant level) can be denoted as:

S (e^{j Ω}) = \frac{N_{0}}{2} = σ_{x}^{2} = P .

(4.44)

This result may be confusing because the values of power and spectral density coincide.

Denoting as $S_{x} (e^{j Ω}) = σ_{x}^{2}$ the PSD of a white noise at the input of a filter $H (e^{j Ω})$ , Eq. (4.39) leads to an output PSD given by

S_{y} (e^{j Ω}) = σ_{x}^{2} | H (e^{j Ω}) |^{2} .

(4.45)

Eq. (4.45) suggests that the output PSD $S_{y} (e^{j Ω})$ has its shape $| H (e^{j Ω}) |^{2}$ imposed by the filter, given that the input PSD $σ_{x}^{2}$ is simply a scaling factor.

Example 4.8. Generation of uniform and Gaussian white noise using Matlab/Octave. A discrete-time white noise with i. i. d. samples is relatively easy to generate in Matlab/Octave using functions that implement random number generators. For example, x=rand(1,1000)-0.5 creates a signal with an autocorrelation that approximates an impulse at the origin and 1,000 samples that are uniformly distributed. The subtraction of 0.5 is necessary to make $μ = 0$ . Similarly, a discrete-time version of WGN (Gaussian, not a uniform distribution) can be generated with x=randn(1,1000). $□$

Converting white noise from continuous to discrete-time

The signals discussed in the previous section were already created in discrete-time. But in some cases the discrete-time white noise is obtained from a continuous-time version or should be interpreted as such.

For example, assume $ν (t)$ is a continuous-time WGN submitted to filtering by an ideal lowpass filter and A/D conversion, as illustrated by the following block diagram:

\begin{array}{l} ν (t) \to h(t) \to A ∕ D \to ν [n] . \end{array}

From Eq. (4.38), the PSD at the output of $h (t)$ is $S (f) = | H (f) |^{2} N_{0} ∕ 2$ . If the filter is ideal and the A/D conversion does not incur in aliasing, the PSD $S (e^{j Ω})$ of $ν [n]$ is a scaled and periodic version of $S (f)$ . Therefore, it is white in discrete-time.

In more details: assume that $h (t)$ is an ideal lowpass filter of bandwidth $BW = F_{s} ∕ 2$ (gain equals to 1 over the band $- F_{s} ∕ 2$ to $F_{s} ∕ 2$ Hz and zero otherwise), where $F_{s}$ is the A/D sampling frequency, then the PSD of the continuous-time signal at the output of $h (t)$ is $S (f) = N_{0} ∕ 2$ over $BW$ and its power is $P = (2 BW) (N_{0} ∕ 2) = BW N_{0}$ . Under the same assumptions of Eq. (1.71), the power values in discrete and continuous-time are the same, such that the power of $ν [n]$ is denoted by its variance $σ^{2} = BW N_{0}$ .

Example 4.9. Discretizing white noise. For example, given that white noise with $N_{0} ∕ 2 = 3$ W/Hz is converted to a discrete-time signal $ν [n]$ via the cascade of an ideal lowpass filter $h (t)$ with passband $BW = F_{s} ∕ 2$ and an A/D process with $F_{s} = 200$ Hz, the power of the signal at the output of the ideal lowpass filter $h (t)$ is

BW N_{0} = \frac{F_{s}}{2} N_{0} = 100 \times 6 = 600 W

and the power of $ν [n]$ is $σ^{2} = BW N_{0} = 600$ W.

Figure 4.25: PSD $S_{x} (f)$ of a continuous-time white noise with $N_{0} ∕ 2 = 3$ W/Hz (top) and its discrete-time counterpart $S_{x} (e^{j Ω})$ obtained with $F_{s} = 200$ Hz (bottom).

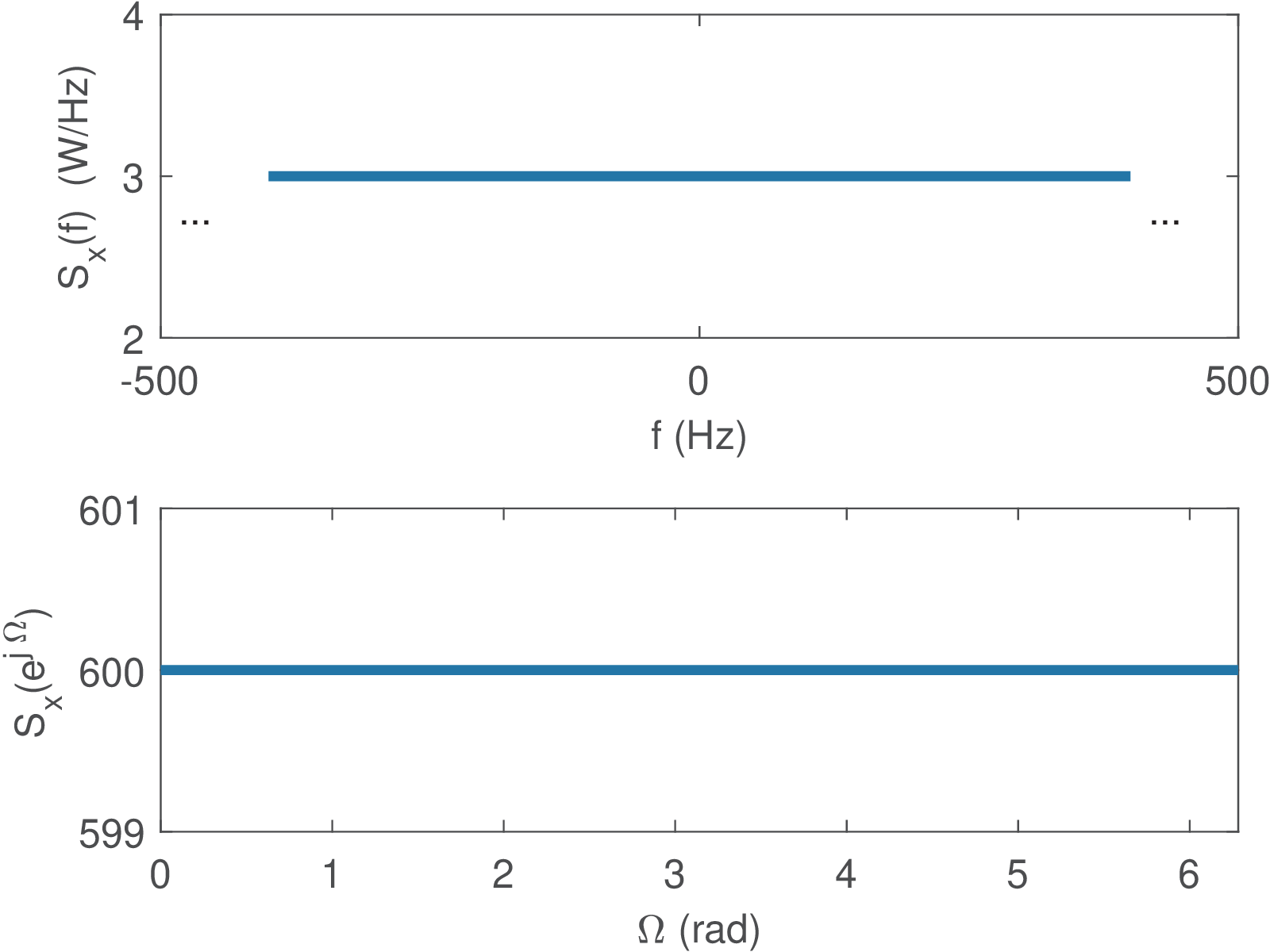
Figure 4.25 depicts the PSD for both continuous and discrete-time signals. Note that the abscissa of $S_{x} (e^{j Ω})$ , which is periodic, is represented from 0 to $2 π$ . As indicated by Eq. (4.21), the power $σ_{x}^{2}$ can be obtained by integrating the density value $S_{x} (e^{j Ω}) ∕ (2 π) = 600 ∕ (2 π)$ watts per radians over the range $[0, 2 π [$ . $□$

Example 4.10. Filtering white noise through systems with unitary-energy impulse responses. Another situation of interest is when white noise is filtered by an LTI that has impulse response $h (t)$ with energy $E_{h} = \int_{- \infty}^{\infty} | h (t) |^{2} d t = 1$ joule, as depicted in:

\begin{array}{l} ν (t) \to h(t) \to x (t) \to A ∕ D \to x [n] . \end{array}

In this case, the Parseval relation of Eq. (A.51) indicates that $E_{h} = \int_{- \infty}^{\infty} | H (f) |^{2} d f = 1$ and from Eq. (4.43), the power of $x (t)$ is

P_{x} = \int_{- \infty}^{\infty} | H (f) |^{2} \frac{N_{0}}{2} d f = \frac{N_{0}}{2} .

(4.46)

Therefore, the power of $x [n]$ is $σ^{2} = N_{0} ∕ 2$ for any $h (t)$ (or, equivalently, any $H (f) = F {h (t)}$ ) if $h (t)$ has energy of 1 joule. However, $x [n]$ will not have a flat PSD unless $h (t)$ is an ideal lowpass filter as in Example 4.9. $□$

Converting white noise from discrete to continuous-time

The conversion of a discrete-time white noise $ν [n]$ into a continuous-time signal $x (t)$ is depicted as:

\begin{array}{l} ν [n] \to D/A \to h(t) \to x (t) . \end{array}

Similar to the previous discussion about white noise C/D conversion in this section, if $h (t)$ is an ideal lowpass filter with passband frequency $F_{s} ∕ 2$ , $x (t)$ has a flat PSD $S_{x} (f)$ with value $N_{0} ∕ 2 = σ^{2} ∕ F_{s}$ , where $σ^{2}$ is the power of $ν [n]$ and $F_{s}$ the sampling frequency. Note that $S_{x} (f) = 0$ for $f > | F_{s} ∕ 2 |$ . Therefore, after filtering $ν [n]$ with an ideal lowpass filter, the resulting $x (t)$ is not a continuous-time WGN, but has a flat PSD within the band $[- F_{s} ∕ 2, F_{s} ∕ 2]$ .

Gaussian signal filtered by LTI system remains Gaussian

If the system is LTI and its input is a realization of a WGN process, then it is well-known from random processes textbooks that the filter output is another Gaussian process. In other words, a Gaussian signal filtered by a linear system remains Gaussian but, in the general case, with a non-white PSD that was shaped by the filter.

When the LTI is an ideal lowpass filter such as in Example 4.9, besides being Gaussian, the output is also flat within the filter passband (or “white” within this band). Hence, when the input is WGN, and $h (t)$ an ideal lowpass filter with passband frequency $F_{s} ∕ 2$ that has its output converted to discrete-time, the resulting $ν [n]$ is a white and Gaussian process with PSD $S (e^{j Ω})$ (again, “white” within the band $- π$ to $π$ rad) and power $σ^{2} = BW N_{0}$ watts, as discussed in Example 4.9.

⁸ Unless otherwise stated, the bandwidth of a signal is assumed to be over non-negative frequencies. But the bandwidth used for some signal processing can include the negative frequencies. This happens when one is calculating the power of a signal based on a bilateral PSD representation.