A.19  Probability and Stochastic Processes

This appendix will provide a very brief overview about key topics. If the reader finds extra time, he/she can find many good textbooks about probability and stochastic (or random) processes.

A.19.1  Joint and Conditional probability

If two events $A$ and $B$ are statistically independent, their joint probability $P(A,B)$ is the multiplication of their individual probabilities: $P(A,B)=P(A)P(B)$. For instance, obtaining two heads when tossing a fair coin twice is $P(H,H)=0.5\times 0.5=0.25$, given that $P(H)=0.5$. Given that the event $B$ is tossing the coin for the second time, we can say that the conditional probability $P(B∕A)$ of $B$ given that the first tossing event $A$ occurred is $P(B∕A)=P(B)$ because $A$ does not influence $B$.

In general, the conditional probability is obtained by its definition: $P(B∕A)=P(A,B)∕P(A)$. Writing this equation as $P(A,B)=P(A)P(B∕A)$, one can imagine a causal relation between $A$ and $B$, with $A$ occurring with $P(A)$, before $B$, and then $B$ occurring with $P(B∕A)$ given that $A$ happened.

Starting from the joint probability $P(A,B)$, one can pick $B$ as the first event that happens and write $P(A,B)=P(B)P(A∕B)$. Combining the two alternatives of writing $P(A,B)$, i. e. $P(A)P(B∕A)=P(B)P(A∕B)$ leads to

which is called the Bayes rule (see, e. g., [ urlBMpro]).

A.19.2  Random variables

First note that the outcome of a probabilistic experiment need not be a number but any element of a set $\mathrm{\Omega }$ of possible outcomes. For example, the outcome when a coin is tossed can be $\omega =$“heads” or $\omega =$“tails”. Basically, random variables allow us to map any probabilistic event into numbers, which are then conveniently manipulated using mathematical operations such as integral and derivatives. A source of confusion is that, strictly, a random variable (e.g., $X$ or $Y$) is a function. More specifically, a random variable (r.v.) is a function $X:\mathrm{\Omega }\to ℝ$ that associates a unique numerical value with every outcome of an experiment (r.v. can be complex numbers, vectors, etc., but here it will be assumed as a real number). In math, a function output is often represented as $y=f(x)$. When dealing with a r.v., instead of adopting something like $X(\omega )$, both the random variable (equivalent to the function $f$) and its output value (equivalent to $y$) is represented by a single letter (e.g., $X$ or $Y$).

There are two types of r.v.: discrete and continuous. Hence, a r.v. has either an associated probability distribution (discrete r.v.) or probability density function (continuous r.v.).

Assume a discrete r.v. $X$ and a continuous r.v. $Y$. While the former is typically described by a probability mass function (pmf), the latter can be described by a probability density function (pdf).

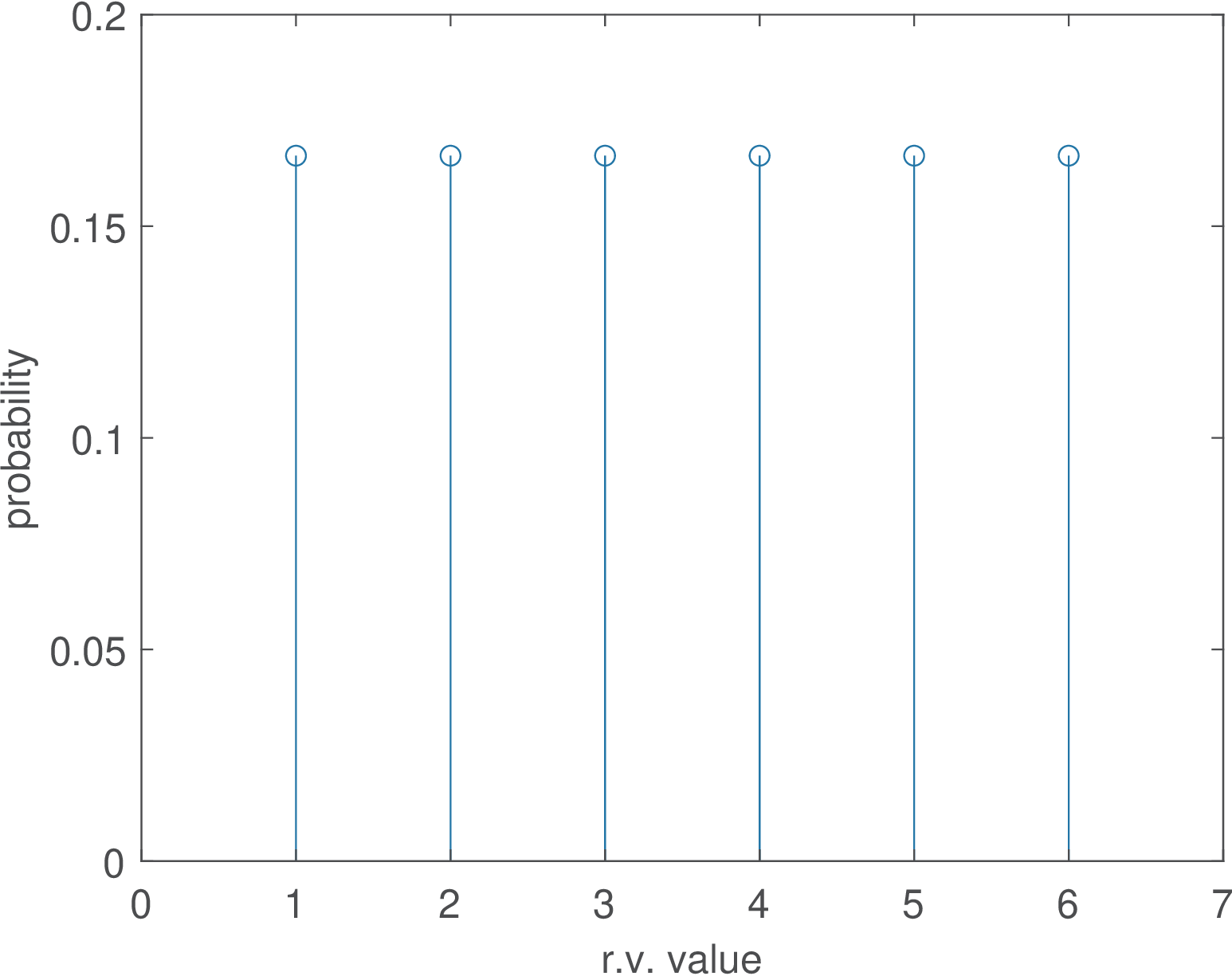
Say that $X$ represents the outcome of rolling a dice. Its PMF is shown in Figure A.7 and indicates that each face of a fair dice has a probability of $1∕6$.

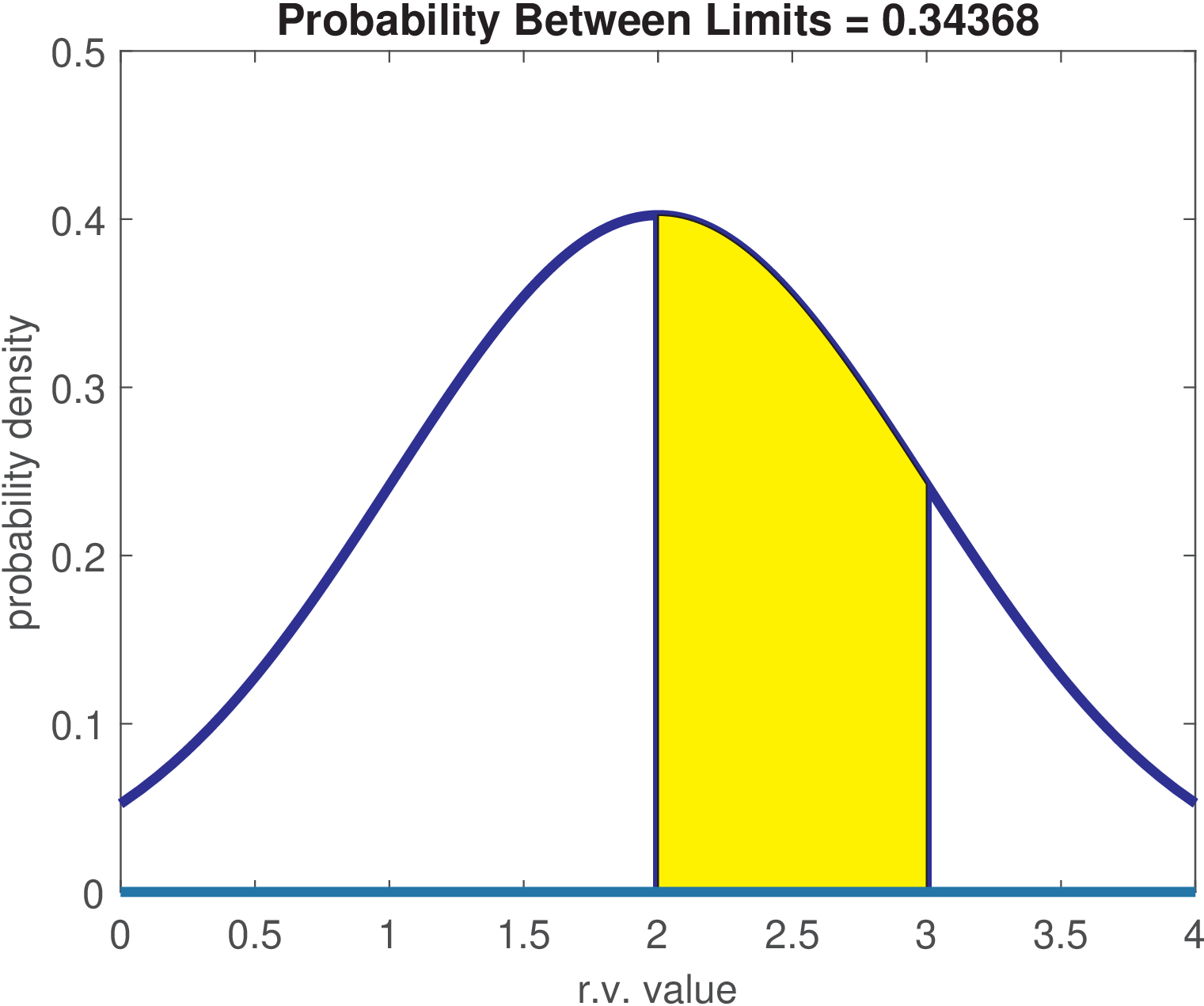
Now consider that $Y$ represents the amplitude of a Gaussian noise source with mean 2 and variance equal to 1. Its pdf is shown in Figure A.8. A common mistake is to assign a non-zero value to a specific value of a density function. For example, it is wrong to say that the probability of $Y=2$ is $0.4$, in spite of this being the value of the function. The function represents a density, and the correct answer is that the probability of $Y=2$, or any other point, is 0. One can extract probability from a pdf only integrating it over a non-zero range of its abscissa. For example, over the range [2, 3] the probability is approximately 0.34 as indicated by the shaded area in Figure A.8.

When dealing with ratios of pdfs it is possible to have the abscissa range ${\mathrm{\Delta }}_x$ canceling out. For example, if a discrete binary r.v. is used to represent two classes (A and B, for example), and each class has a pdf associated to it ($f(\mathbf{\text{x}}|A)$ and $f(\mathbf{\text{x}}|B)$, respectively), the Bayes’ rule states

In this case, ${\mathrm{\Delta }}_x$ cancels because it appears on both numerator and denominator.

A.19.3  Expected value

The expected value $𝔼[\cdot ]$ operator is the most common mathematical formalism for calculating an average (or mean).

The expected value is a linear operator (see Appendix A.27.1 for more information about linearity), such that

The expected value $𝔼[X]$ of a random variable $X$ can be estimated as a typical average when $X$ can be represented by a finite-dimension vector. For example, if $\mathbf{\text{x}}=[3,5,4,4,5,3]$ is a vector with random samples from $X$, the expected value $𝔼[X]$ can be estimated as $𝔼[X]\approx \overline{\mathbf{\text{x}}}=(3+5+4+4+5+3)∕6=4$, where $\overline{\mathbf{\text{x}}}$ is the conventional mean value.

If one has realizations of a random variable $X$, for instance organized as a vector $\mathbf{\text{x}}$, and is looking for the expected value $𝔼[g(X)]$ of a function $g(X)$, it is possible to apply the function $g(\cdot )$ to each realization (value of $\mathbf{\text{x}}$) and then take their average. For example, assume $g(X)=X^2$ and one is interested on estimating $𝔼[X^2]$ based on realizations $\mathbf{\text{x}}=[-1,3,-3,4,-2]$ of $X$. In this case, applying $g(X)=X^2$ to elements of $\mathbf{\text{x}}$ leads to the vector $\mathbf{\text{y}}=[{(-1)}^2,3^2,{(-3)}^2,4^2,{(-2)}^2]$, which has the average $\overline{\mathbf{\text{y}}}=(1+9+9+16+4)∕5=7.8$. The estimate is $𝔼[X^2]\approx \overline{\mathbf{\text{y}}}=7.8$.

As another example, consider ${\mu }_x=𝔼[X]$ is known (or has been previously estimated), and one is interested on estimating the variance $𝔼[{(X-{\mu }_x)}^2]$. In this case, $g(X)={(X-{\mu }_x)}^2$ and if the realizations are still $\mathbf{\text{x}}=[-1,3,-3,4,-2]$, which has an average ${\mu }_x=0.2$, applying $f(X)$ leads to a vector $\mathbf{\text{z}}=[{(-1-0.2)}^2,{(3-0.2)}^2,{(-3-0.2)}^2,{(4-0.2)}^2,{(-2-0.2)}^2]$ with mean value $\overline{\mathbf{\text{z}}}=7.76$. In this case the estimated variance is $𝔼[{(X-{\mu }_x)}^2]\approx \overline{\mathbf{\text{z}}}=7.76$.

The variance is often denoted as ${\sigma }_x^2$, and can be written as

which is often interpreted as $𝔼[X^2]={\sigma }_x^2+{\mu }_x^2$.

When a discrete random variable $X$ has $V$ distinct values, its mean $𝔼[X]$ can be estimated with

where $p_i$ is the probability of the $i$-th possible value $x_i$. For instance, the realizations $\mathbf{\text{x}}=[3,5,4,4,5,3]$ have only $V=3$ distinct values: $x_1=3,x_2=4$ and $x_3=5$, each one with estimated probability $p_i=1∕3,\forall <!--\; FUNCTION\; APPLICATION\; -->i$. Hence,

The same result could be obtained by directly taking the mean value of the $N=6$ elements with

Note that $x[n]$ corresponds to the $n$-th element in $\mathbf{\text{x}}$, while $x_i$ is the $i$-th distinct value of $\mathbf{\text{x}}$.

When $X\in ℝ$ is a continuous random variable, instead of Eq. (A.68) one has its continuous version:

where $f_X(x)$ is the probability density function of $X$. In this case, for each value of $x$, the role of the probability $p_i$ in the discrete r.v. case, is played by the value $f_X(x)$ that corresponds to a “weight” that depends on the likelihood of the specific value $x$.

In order to find $𝔼[g(X)]$ for a given function $g(\cdot )$ one can use:

A.19.4  Orthogonal versus uncorrelated

Two random variables $X$ and $Y$ are said to be orthogonal to each other if

They are said to be uncorrelated with each other if

The above condition is equivalent to

Note that if one or both of $X$ and $Y$ have zero mean, then the orthogonal and uncorrelated conditions are equivalent.

A.19.5  PDF of a sum of two independent random variables

If $X$ and $Y$ are independent, $Z=X+Y$ implies $f(z)=f(x)\ast f(y)$. For example, the sum of a bipolar signal (-5 and +5V with 0.5 of probability each) with pdf $f_x(x)=0.5[\delta (x-5)+\delta (x+5)]$ and additive white Gausssian noise (AWGN) with pdf $f_y(y)$ is a good example because the result is the Gaussian scaled by 0.5 and shifted to the position of each of the original impulses, at $-5$ and 5, i. e., $f_z(z)=0.5[f_y(z-5)+f_y(z+5)]$.