Fixed and Floating-Point Number Representations

A.28 Fixed and Floating-Point Number Representations

A.28.1 Representing numbers in fixed-point

Both fixed and floating-point representations are capable of representing real numbers. A real number can be written as the sum of an integer part and a fractional part that is less than one and non-negative.

The name “fixed-point” is due to the fact that the $b$ bits available to represent a number are organized as follows:

1 bit representing the sign (positive or negative) of the integer part and, consequently, of the number itself
$b_{i}$ bits representing the integer part of the number
$b_{f}$ bits representing the fractional part of the number

such that $b = b_{i} + b_{f} + 1$ bits. For simplicity, the sign bit is assumed here to be the MSB, but in practice that depends on the adopted standard and the machine endianness (see Appendix B.2.3 for a brief explanation of big and little endian formats).

One way of thinking the “point” is that there is flexibility on choosing the power of 2 that is associated to the second bit, at the right of the MSB. After this design choice is made, a fictitious point separates the bits corresponding to the integer part from the fractional part bits. There is a convention of denoting the values chosen for $b_{i}$ and $b_{f}$ as Q $b_{i}$ . $b_{f}$ .

Figure A.37: Fixed-point representation Q3.4 of the real number 5.0625. The “point” is always after the bit corresponding to the weight $2^{0}$ .

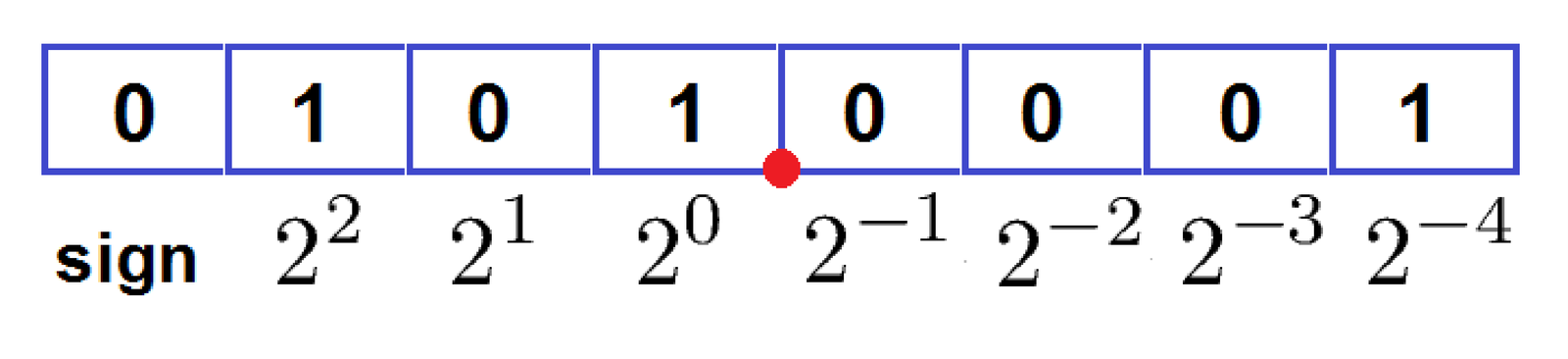
Figure A.37 shows an example of fixed-point representation using Q3.4, for which $b_{i} = 3$ , $b_{f} = 4$ and, consequently $b = 8$ . In this case, the point is located between the fourth and fifth bits. The binary codeword $x_{b} = 01010001$ is mapped to a real number according to the position of the point:

1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0} + 0 \times 2^{- 1} + 0 \times 2^{- 2} + 0 \times 2^{- 3} + 1 \times 2^{- 4} = 5.0625 .

It is very common to normalize the numbers to make them fit the range $[- 1, 1 [$ . In this case $b_{i}$ can be zero, $b_{f} = b - 1$ and the second bit has a weight in base-2 equals to $2^{- 1}$ such that the point is between the MSB and this bit. The other bit weights are then $2^{- 2}, \dots, 2^{- b_{f}}$ , according to their respective position. For example, the outputs of a quantizer with $b = 2$ bits when represented in the format Q0.1 ( $b_{i} = 0$ , $b_{f} = 1$ ) assume four possible outputs $x_{q} \in {- 1, - 0.5, 0, 0.5}$ . In general, the weight $2^{- b_{f}}$ of the LSB corresponds to the value of the step size, i. e.

Δ = 2^{- b_{f}} .

(A.124)

Note that the number 5.0625 in Figure A.37 can also be obtained by identifying that $x_{b}$ corresponds to $x_{i} = 81$ and calculating $x_{q} = x_{i} Δ = 81 \times 2^{- 4} = 5.0625$ . If the point were moved to the position between the MSB and second bit, which corresponds to choosing Q0.7, the quantizer would have $Δ = 2^{- 7}$ and the same codeword $x_{b} = 01010001$ would be mapped to $x_{q} = 0.6328125$ .

In summary, when a fixed-point representation is assumed, the quantizer has step $Δ = 2^{- b_{f}}$ and can output numbers in the range $[- 2^{b_{i}}, 2^{b_{i}} - Δ]$ . Algorithm 1 describes the process for representing a real number $x$ in fixed-point using Q $b_{i}$ . $b_{f}$ .

______________________________________________________________________________ Algorithm 1: Fixed-point conversion._________________________________________________________ Input:

x

b_{i}

b_{f}

// value to quantize, integer and fractional # bits Output:

x_{b}

x_{i}

x_{q}

// binary, integer and decoded forms of

Q {x}

x_{i} = x ∕ Δ

// Equivalent to multiplying by

1 ∕ Δ = 2^{b_{f}}

2if

x_{i}

is not an integer then 3 4 5round

x_{i}

to the nearest integer // floor is sometimes used instead 6if

x_{i} < - 2^{b_{i}}

then 7 8 9

x_{i} = - 2^{b_{i}}

// Implement saturation for negative values 10Print: Warning! Consider increasing number

b_{i}

of integer bits 11if

x_{i} > 2^{b_{i}} - Δ

then 12 13 14

x_{i} = 2^{b_{i}} - Δ

// Implement saturation for positive values 15Print: Warning! Consider increasing number

b_{i}

of integer bits 16

x_{q} = x_{i} \times Δ

// Multiply by

Δ

to find decoded value 17if

x_{i} < 0

then 18 19 20Obtain

x_{b}

using two’s complement // with

b

bits and sign extension 21else 22 23 24Simply obtain

x_{b}

as the standard-positive binary coding of

x_{i}

___

For example, using Algorithm 1 to represent $x = - 7.45$ in Q3.4, the first step is to calculate $x ∕ Δ = - 7.45 \times 2^{4} = - 119.2$ . Then, using round leads to $x_{i} = - 119$ , which corresponds to $x_{q} = - 7.4375$ and $x_{b} = 10001001$ in two’s complement. This algorithm is the same implemented in Listing 1.18 but explicitly outputs the binary codeword $x_{b}$ .

Choosing the point position depends on the dynamic range of the numbers that will be represented and processed. This is typically done with the help of simulations and is a challenging task due to the tradeoff between range (the larger $b_{i}$ the better) and precision (the larger $b_{f}$ the better). In sophisticated algorithms, it is typically required to assume distinct positions for the point at different stages of the process. In such cases, using specialized tools such as Mathwork’s Fixed-Point Designer [ url1mfi] can significantly help.

Example A.13. Fixed-point in Matlab and Octave. Both Matlab and Octave have toolboxes for fixed-point arithmetic. But, unfortunately, they are not compatible. Matlab’s Fixed-Point Toolbox is more sophisticated and better documented. If you have the Matlab’s toolbox, try for example doc fi. The Matlab command for representing $x = - 7.45$ as in the previous example is:

1x=-7.45;signed=1;b=8;bf=4;x_q=fi(x,signed,b,bf)

which outputs:

x_q = -7.437500000000000
          DataTypeMode: Fixed-point: binary point scaling
                Signed: true
            WordLength: 8
        FractionLength: 4
             RoundMode: nearest
          OverflowMode: saturate
           ProductMode: FullPrecision
  MaxProductWordLength: 128
               SumMode: FullPrecision
      MaxSumWordLength: 128
         CastBeforeSum: true

Example A.14. Quantization example in Matlab. As another example, let $x (t_{0}) = 2804.6542$ volts be the amplitude of $x (t)$ at $t = t_{0}$ , such that $x [n_{0}] = 2804.6542$ , where $n_{0}$ is the value of $n$ corresponding to $t = n_{0} T_{s}$ . The value of $x [n_{0}]$ quantized with $b = 16$ bits and reserving $b_{i} = 12$ bits to the integer part is $x_{q} [n_{0}] = Q {x [n_{0}]} = 2804.625$ , which can be obtained in Matlab with:

1format long %to better visualize numbers 
2x=2804.6542; %define x 
3xq=fi(x) %quantize with 16 bits and "best-precision" fraction length

When fi is used with a single argument, it assumes a 16-bit word length and it adjusts $b_{f}$ such that the integer part of the number can be represented (called in Matlab “best-precision” fraction length). For this example, the result is:

      xq = 2.804625000000000e+03
      Signedness: Signed
      WordLength: 16
      FractionLength: 3

indicating that $b_{i} = 12$ bits are used to represent the integer part of $x$ (2084), given that $2^{11} = 2048 < x < 2^{12} = 4096$ . Considering one bit is reserved for the sign, then $b_{f} = 16 - 1 - b_{i} = 3$ bits, which is the FractionLength. $□$

Octave users have to look after the Fixed Point Toolbox for Octave.²⁵ Its syntax is a = fixed(bi, bf, x), where a is an object of class FixedPoint. The class field a.x stores the value in the regular floating point format.²⁶ The Octave command for representing $x = - 7.45$ as in the previous example is:

1x=-7.45;bi=3;bf=4;x_q=fixed(bi,bf,x)

It should be noted that the following commands bi=0; bf=1;a=fixed(bi,bf,0.4) output a=0 because fixed implements truncation (to 0) instead of rounding (to $Δ = 0.5$ in this case). As another example, c=fixed(bi,bf,-0.6) outputs c=-1 ( $- 0.6$ was truncated to $- 1$ ). Following object-oriented programming (OOP) practice, one should be consistent when dealing with the objects. For example, a+4 returns an error message because a is an object, not a number, and a.x+4 should be used instead. On the other hand, a+c is a valid operation that returns $- 1$ when the objects were created with the previous commands. $□$

A.28.2 IEEE 754 floating-point standard

Choosing the point position provides a degree of freedom for trading off range and precision in a fixed-point representation. However, there are situations in which a software needs to deal simultaneously with small and large numbers, and having distinct positions for the point all over the software is not practical or efficient. For example, if distances in both nanometers and kilometers should be manipulated with reasonable precision, the dynamic range of $1 0^{3} ∕ 1 0^{- 9} = 1 0^{12}$ would require $b_{i} > 40$ bits for the integer part or keeping track of two distinct point positions. Hence, in many cases, a floating-point representation is more adequate.

A number in floating point is represented as in scientific notation:

x_{q} = significand \times {base}^{exponent} .

(A.125)

For example, assuming the base is 10 for simplicity, the number $x_{q} = 123.4567$ is interpreted as $x_{q} = 1.234567 \times 1 0^{2}$ , where 1.234567 is the significand and 2 the exponent. While in fixed point the $b - 1$ bits available to represent a signed number are split between $b_{i}$ and $b_{f}$ , in floating point the $b$ bits are split between the significand and exponent.

The key aspect of Eq. (A.125) is that, as the value of the exponent changes, the “point” has new positions and allows to play a different trade off between range and precision: the values a floating point $x_{q}$ can assume are not uniformly spaced. While fixed-point numbers are uniformly spaced by $Δ = 2^{- b_{f}}$ , which then imposes the maximum error within the range, the error magnitude in a floating point representation depends on the value of the exponent. For a given error in the significand representation, the larger the exponent, the larger the absolute error of $x_{q}$ with respect to the number it represents. This is a desired feature in many applications and floating point is used for example in all personal computers. The fixed point niche are embedded systems, where power consumption and cost have more stringent requirements.

The IEEE 754 standard for representing numbers and performing arithmetics in floating point is adopted in almost all computing platforms. Among other features,²⁷ it provides support to single and double precision, which are typically called “float” and “double”, respectively, in programming languages such as C and Java.

The wide adoption of IEEE 754 is convenient because a binary file written with a given language in a given platform can be easily read with a distinct language in another platform. In this case, the only concern is to make sure the endianness is the same (Appendix B.2.3). The two following examples discuss numerical errors and quantization in practical scenarios.

Example A.15. Floating point representation in Matlab/Octave and numerical errors. Unless specified otherwise, Matlab/Octave uses double precision. For example, the commands clear all;x=3;whos generate the following output:

Variables in the current scope:
   Attr Name        Size                     Bytes  Class
   ==== ====        ====                     =====  =====
        x           1x1                          8  double
Total is 1 element using 8 bytes

in Octave and equivalent information in Matlab. As indicated, numbers in double precision use $b = 64$ bits while $b = 32$ are used in single precision (“float”). A double allocates 11 bits to the exponent and 52 to the significand, while in float precision these numbers are 8 and 23, respectively. The sign bit is used for the significand, but the exponent can also be a positive or negative number. Hence, one can consider that one exponent bit is used to represent its own sign.

The following Matlab/Octave code can be used to investigate the ranges for single and double precision:

Listing A.16: MatlabOctaveCodeSnippets/snip_signals_data_precision.m

1str = 'Ranges for double before and after 0:\n%g to %g and %g to %g'; 
2sprintf(str, -realmax, -realmin, realmin, realmax) 
3str = 'Ranges for float before and after 0:\n%g to %g and %g to %g'; 
4sprintf(str,-realmax('single'),-realmin('single'), ... 
5    realmin('single'), realmax('single'))

The output is:

ans = Ranges for double before and after 0:
-1.79769e+308 to -2.22507e-308 and 2.22507e-308 to 1.79769e+308
ans = Ranges for float before and after 0:
-3.40282e+038 to -1.17549e-038 and 1.17549e-038 to 3.40282e+038

From this output, it would be a mistake to consider that $Δ = 2.22507 \times 1 0^{- 308}$ and $1.17549 \times 1 0^{- 038}$ for double and single precision, respectively. Recall that the floating point numbers are non-uniformly spaced.

Figure A.38: Comparison of step sizes for IEEE 754 floating points with single and double precision in the range $[- 8, 8]$ . Note as $Δ (x)$ increases with $| x |$ .

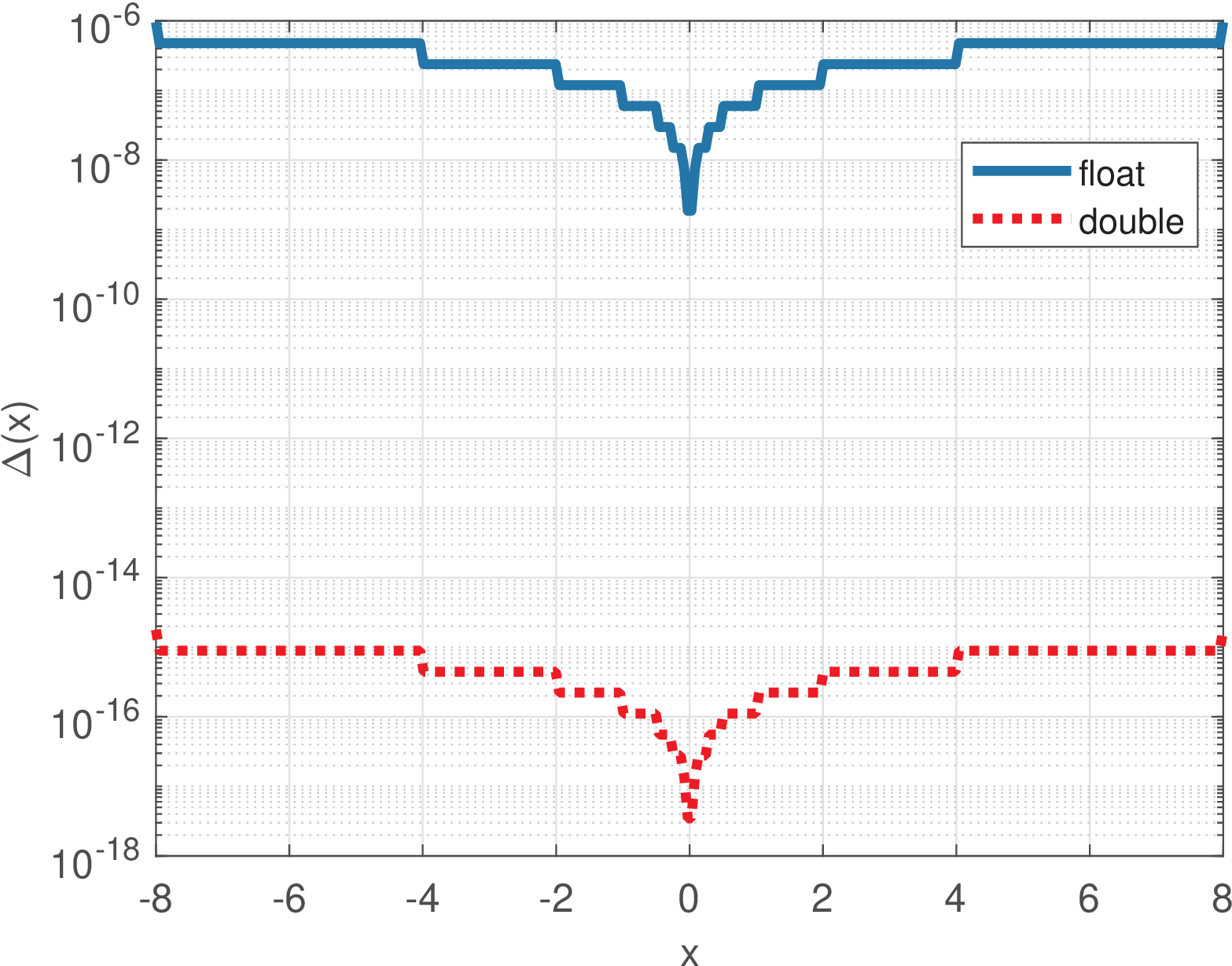
Given that the step $Δ (x)$ varies from a number $x$ to the next number $x + Δ (x)$ in floating point, Matlab/Octave provides the command eps(x) to obtain $Δ (x)$ . Figure A.38 provides a comparison obtained with Listing A.17.

Listing A.17: MatlabOctaveCodeSnippets/snip_signals_delta_calculation.m

1N=300; delta_x=zeros(1,N); x=linspace(-8,8,N); %define range 
2%use loops to be compatible with Octave. Matlab allows delta_x=eps(x) 
3for i=1:N, delta_x(i) = eps(single(x(i))); end %single precision 
4semilogy(x,delta_x); hold on 
5for i=1:N, delta_x(i) = eps(x(i)); end  %double precision 
6semilogy(x,delta_x,'r:'); legend('float','double'); grid

Figure A.38 indicates that care must be exercised especially when dealing with single precision, which is a requirement of many DSP chips, for example. Even double precision can cause strange behavior. A good example is provided by Listing A.18, from Mathwork’s documentation [ url1flm].

Listing A.18: MatlabOctaveCodeSnippets/snip_signals_numerical_error.m

1a = 0.0; %a uses double precision 
2for i = 1:20 
3  a = a + 0.1; %20 times 0.1 should be equal to 2 
4end 
5a == 2 %checking if a is 2 returns false due to numerical errors

The design of algorithms that are robust to numerical errors, such as matrix inversion, is the focus of many textbooks. Besides trying to adopt robust algorithms, a DSP programmer needs to always be aware of the possibility of numerical errors. Taking the example of the previous code, instead of a check such as if (a==2), it is often better to write

1if abs(a-2) < eps %check if a is 2 (consider numerical errors)

where eps corresponds to eps(1) and is the default when a better guess for the range of interest (eps(2) in the example) is not available.

It is possible to instruct Matlab/Octave to use single (using the function single) or double precision (the default) as illustrated in Listing A.19, which uses the FFT algorithm (to be discussed in Chapter 2) to compare the options with respect to speed.

Listing A.19: MatlabOctaveCodeSnippets/snip_signals_single_precision.m

1N=2^20; %FFT length (one may try different values) 
2xs=single(randn(1,N)); %generate random signal using single precision 
3xd=randn(1,N); %generate random signal using double precision 
4tic %start time counter 
5Xs=fft(xs); %calculate FFT with single precision 
6disp('Single precision: '), toc %stop time counter 
7tic %start time counter 
8Xd=fft(xd); %calculate FFT with double precision 
9disp('Double precision: '), toc %stop time counter

Note that benchmarking is tricky and using single precision may not be faster than double precision. On a given laptop, Listing A.19 executed on Matlab returned 0.073124 and 0.104728 seconds, which indicates that double precision was approximately 1.43 times slower than single precision. Executing the code on the same machine using Octave led to approximately 0.06 seconds to both double and single precision. $□$

²⁵ Version 0.7.10 is relatively old (2004) and is currently not part of Octave-Forge, but there are interested users [ url1fix].

²⁶ The command whos allows to inspect the variable classes / types.

²⁷ See, e. g., [ url1flo] for more details.