Q function

A.5 Q function

One just needs to know $Q (x)$ for positive $x$ because

$Q (- x) = 1 - Q (x)$ (A.16)
When expressed in dB, it is used $20 {log}_{10} (x)$ .
$Q (x) = 0.5 erfc (x ∕ \sqrt{2})$ , where erfc is the complimentary error function.
Matlab provides the qfunc in the comm toolbox. In case this toolbox is not available or using Octave, it is possible to use the erfc function as follows: y = 0.5*erfc(x/sqrt(2)). See ak_qfunc.m and ak_qfuncinv.m.

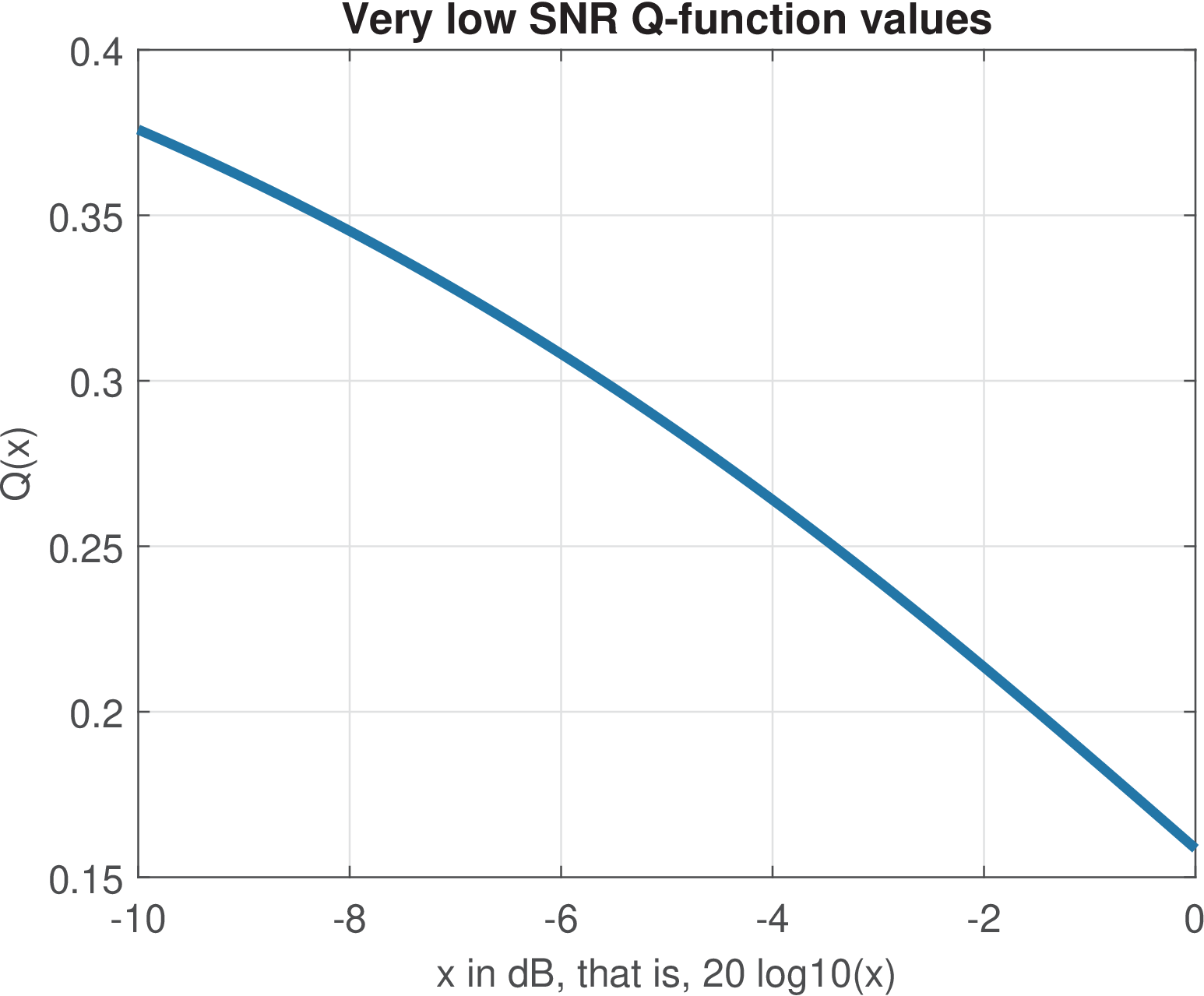
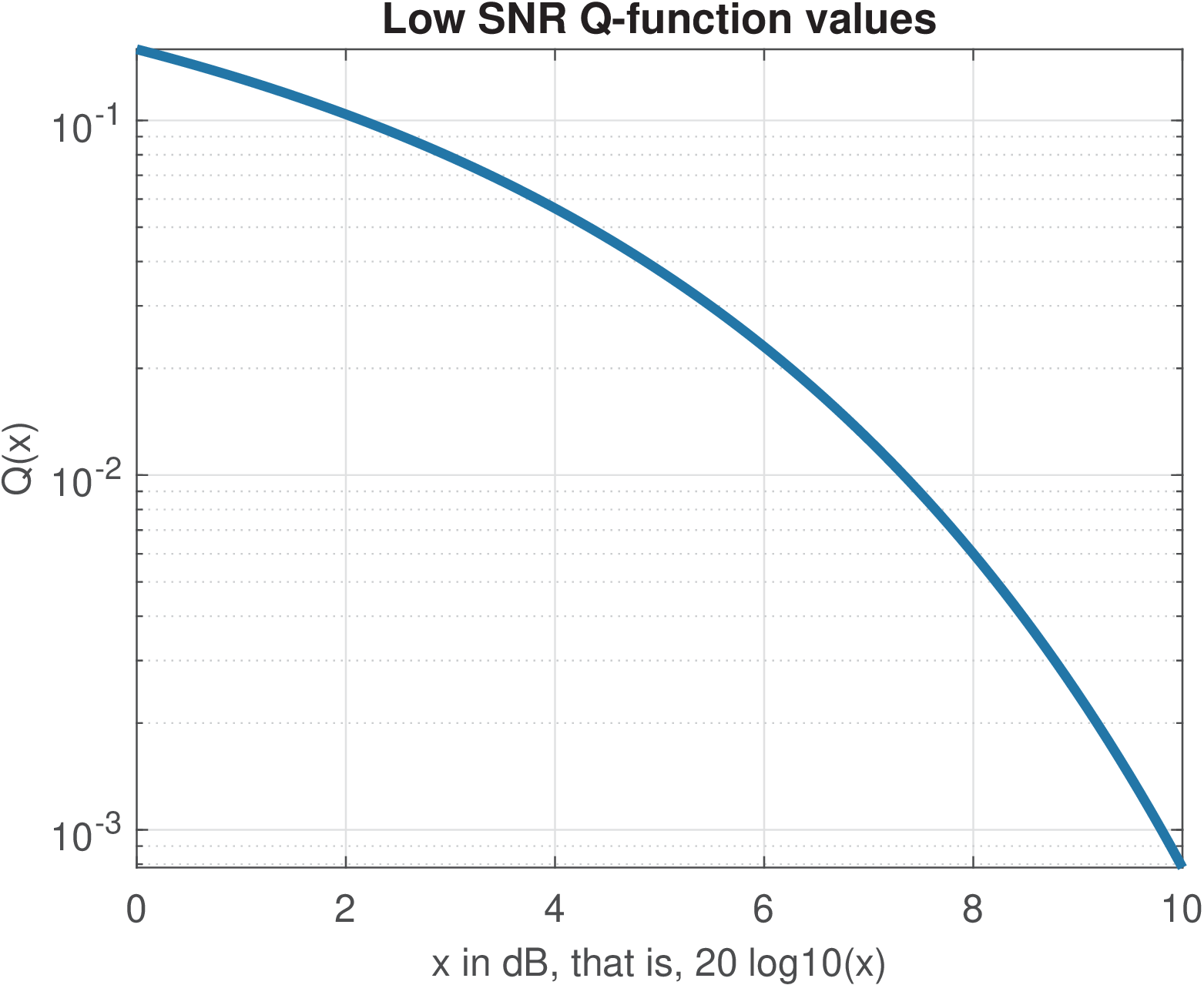
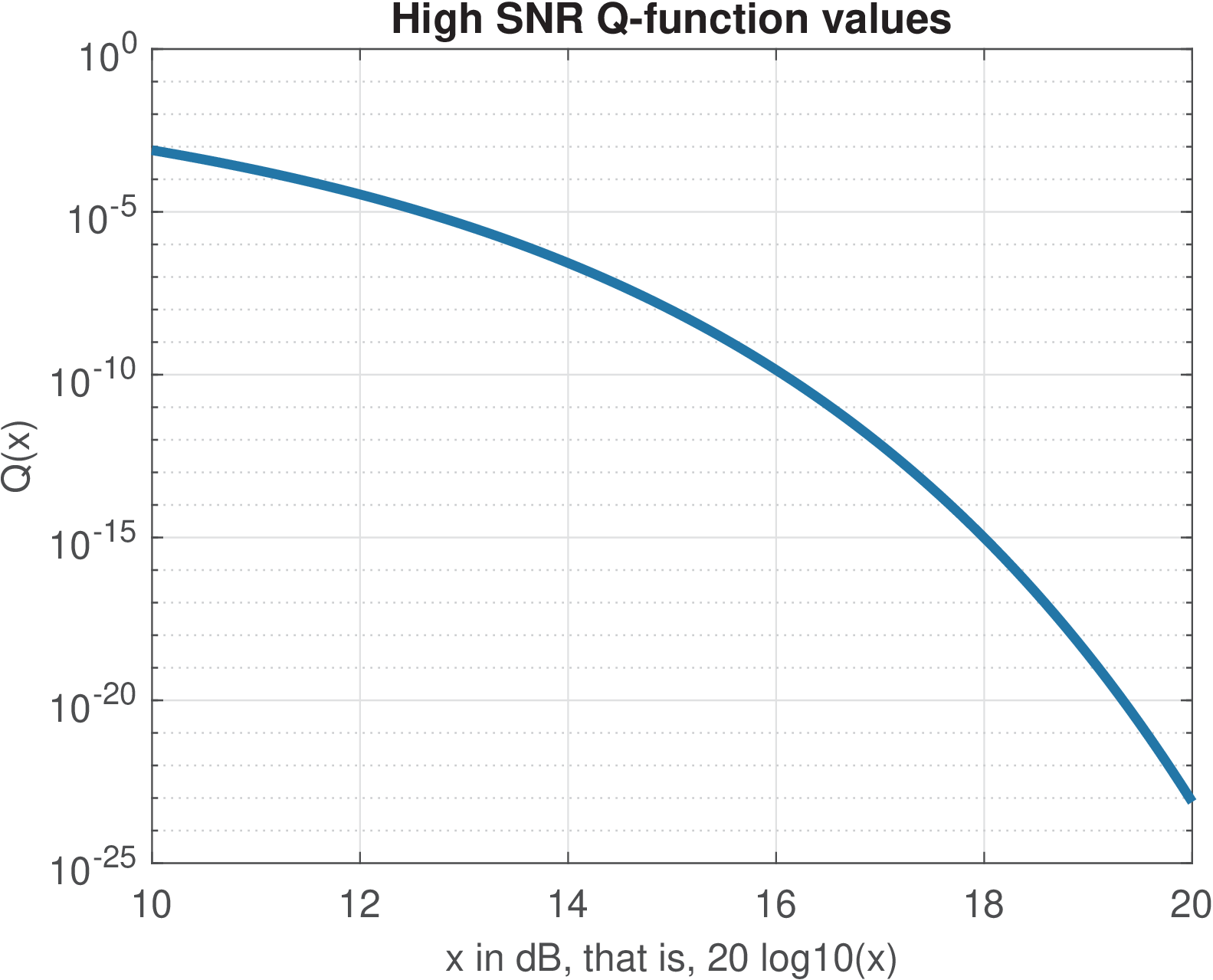
The Q values for three different ranges of its argument are shown in Figure A.1(a), Figure A.1(b) and Figure A.1(c).

Figure A.1: Q function for three different SNR ranges.

A Q function approximation that is good for $x > 3$ :

Q (x) \approx \frac{1}{x \sqrt{2 π}} exp (- \frac{x^{2}}{2})

(A.17)

An accurate approximation (less than 1.2% of error) is:

Q (x) \approx [\frac{1}{\frac{π - 1}{π} x + \frac{1}{π} \sqrt{x^{2} + 2 π}}] \frac{1}{\sqrt{2 π}} exp (- \frac{x^{2}}{2}) .

(A.18)

The expression is valid for $x \geq 0$ and for $x < 0$ one should use $Q (- x) = 1 - Q (x)$ . The function ak_qfuncApprox implements Eq. (A.18). In case you have Matlab, the code below compares it with Matlab’s qfunc.

1x=-3:0.01:3; %define a range for x 
2qx1=ak_qfuncApprox(x); %use the approximation 
3qx2=qfunc(x); %qfunc in Matlab's Communication Toolbox 
4plot(x,100*(qx1-qx2)./qx2); %get error in % 
5grid, xlabel('x'); ylabel('Error in Q approximation (%)')