1.13  Applications

Some applications of the main results in this chapter are discussed in this section.

Application 1.1. Recording signals with a sound board and the Audacity software. It is relatively easy to record sound using a microcomputer. However, most softwares that capture sound are not very useful for DSP applications, because they assume the user is not interested in “low-level” details such as the number of bits per sample. But there many alternatives that do provide this kind of information. Two free and open-source (FOSS) softwares for manipulation sound files are Audacity [ url1aud] and Sox [ url1sox]. While Sox is very useful for converting among file formats and working from a command line, Audacity is adopted here because it has a graphical user interface (GUI) that allows, for example, to monitor recording and avoid saturating the ADC, which would distort the sound due to clipping of its amplitudes.

Figure 1.59 shows a short segment of audio recorded with the default options of sampling frequency $F_s=44.1$ kHz and number $b=32$ bits per sample in floating-point, as indicated by the letter A in the figure. The menu Edit - Preferences - Quality of Audacity allows to change these values. Another option to change $F_s$ is the “Project rate” in letter B of Figure 1.59. The level meters indicated with letter C are activated during recording and playback and, in this case, suggest that the signal amplitude was clipped due to ADC saturation. Alternatively, this can be visualized using menu View - Show Clipping. Each time a new recording starts (by clicking the button indicated by letter D), the audio track has the $F_s$ and $b$ imposed by the current default options. Most sound boards have two channels and can record in stereo but here it is assumed that only one channel is of interest and the files are mono.

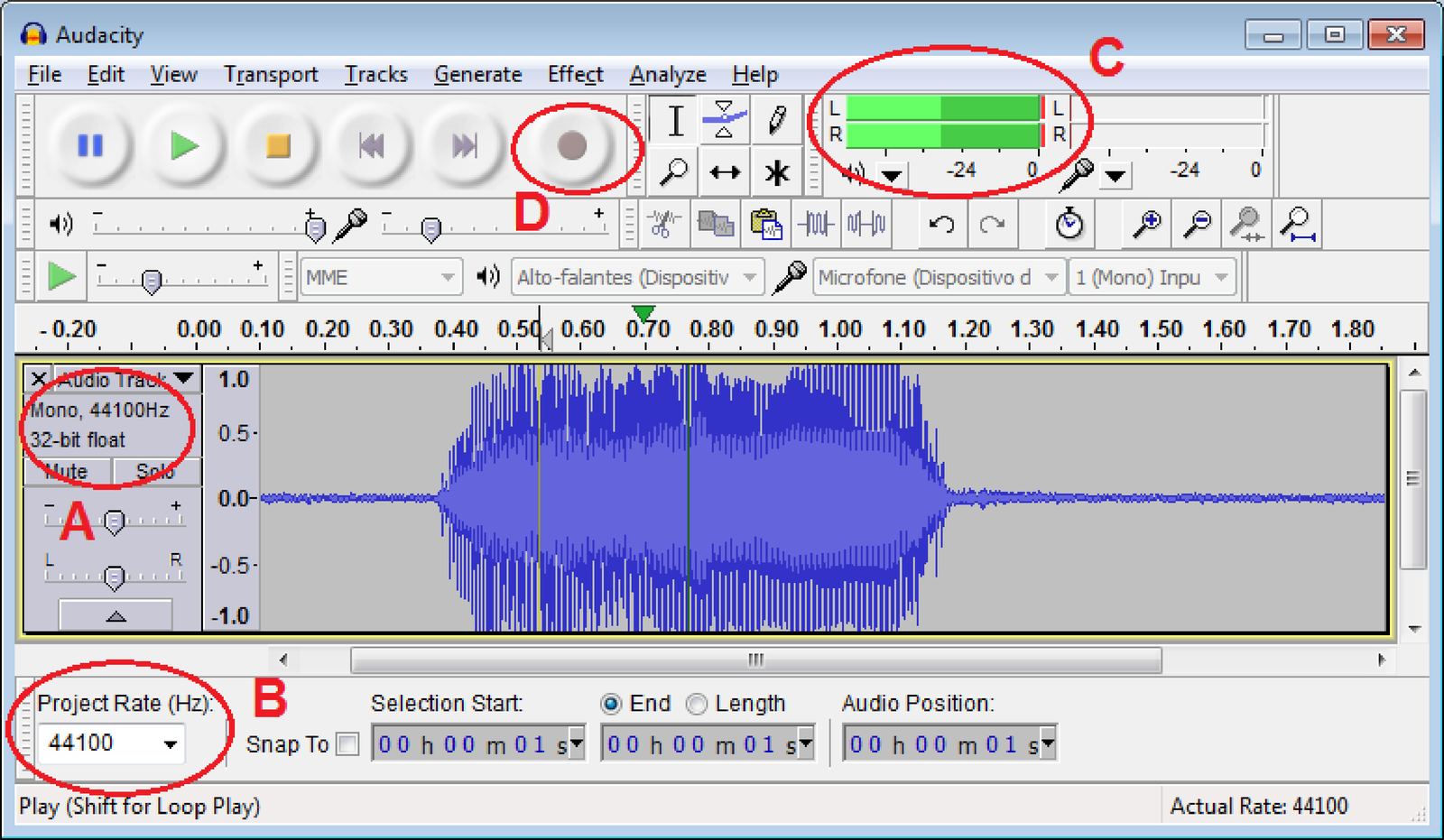
Audacity can save a signal in a variety of file formats, such as MP3, using the menu Export. Our goal is to later read the saved file in another software (Matlab/Octave, etc.), so MP3 should be avoided and of special interest here are “wav” (actually the WAVE format, an instance of Microsoft’s RIFF file format) and raw (header-less).

The “wav” format is just a wrapper for many codecs. In other words, within a “wav” file one can find uncompressed data requiring hundreds of kilobits to represent each second (kbps) of audio as well highly compressed data requesting less than five kbps. Unless the file size should be minimized, for increased portability it is better to use an uncompressed “PCM” format. Due to its adoption in digital communications, the result of A/D conversion is sometimes called pulse-coded modulation (PCM). Hence, PCM can be seen as a codec but its output is equivalent to a signal simply sampled at $F_s$ and quantized (or encoded) with $b$ bits/sample. If the adopted quantizer is uniform (see Eq. (1.41)), the PCM is called linear. The linear PCM is the best format with respect to portability but there are also two popular non-linear PCMs.

Because the probability distribution of long segments of speech signals is approximately Laplacian, not uniform, the quantizer used in digital telephony is non-uniform. These quantizers are based on non-linear curves (approximately logarithmic) called A-law and $\mu$-law. Figure 1.60 shows some options when the user chooses Export - Other compressed files (in “type”) and then Options.

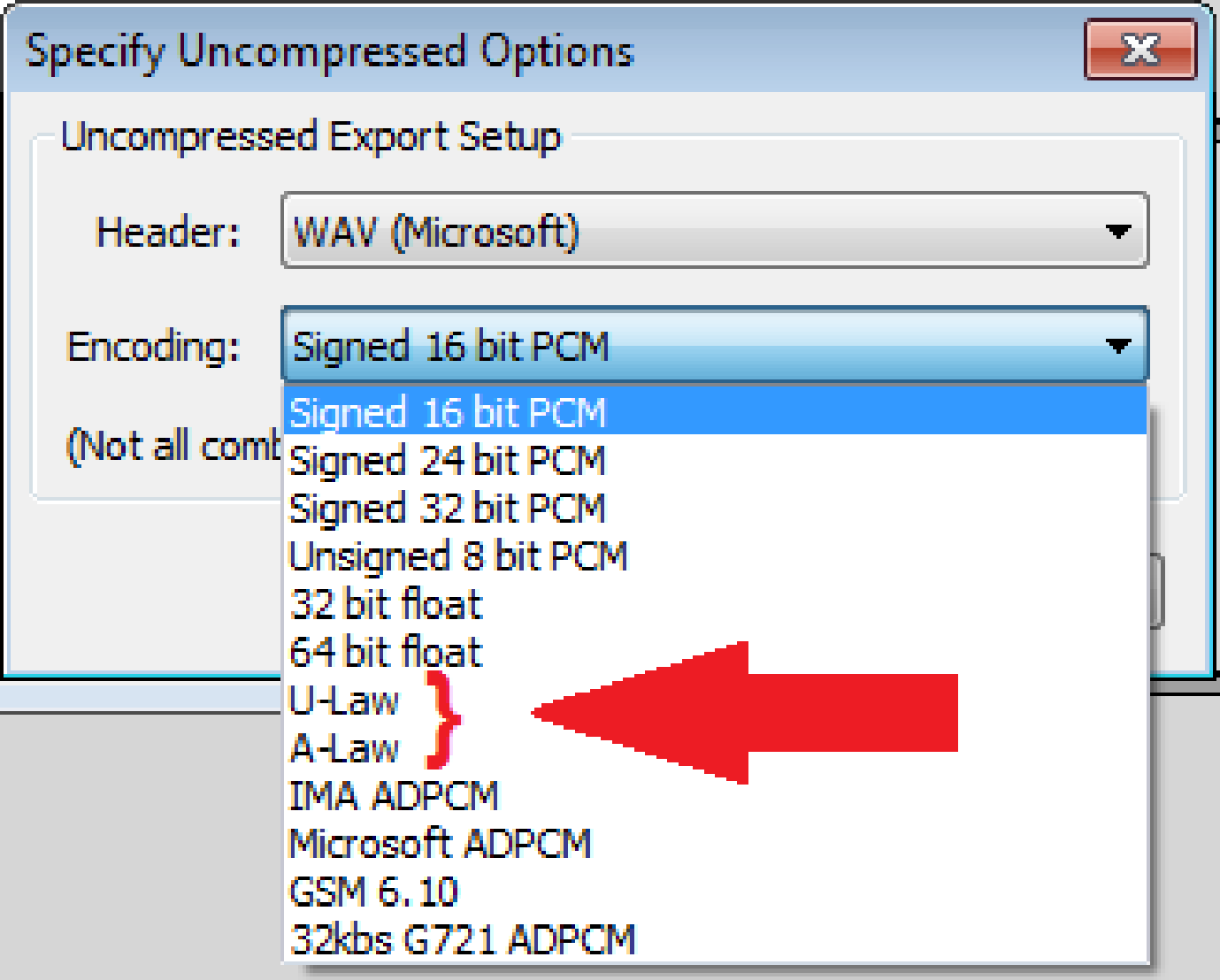
Hence, use Audacity to record some sound with $F_s=8$ kHz and export it as a file named myvoice.wav in the “WAV (Microsoft) signed 16 bits” format. After that, read it with Matlab/Octave using:

1[x,Fs,wmode,fidx]=readwav('myvoice.wav'); 
2b = fidx(7); % num of bits per sample

It can be observed that Fs=8000 and b=16, as recorded. Note that by default the readwav function outputs samples in floating-point and normalizes them to be within the range $[-1,1]$. If the actual integer values are of interest, Matlab allows to use

1[x2,Fs,wmode,fidx]=readwav('myvoice.wav','r'); % get raw samples 
2b = fidx(7); % num of bits per sample

Using the previous commands and comparing min(x), max(x) and min(x2), max(x2), in the case of a specific audio file, the (native) integer values $-8488$ (min) and 5877 (max) were normalized to $-0.2590$ and 0.1794, respectively, when not using the option ’r’. The normalization consists in dividing the native integer values by $2^{b-1}$, which takes in account that these values are originally within the range $[-2^{b-1},2^{b-1}-1]$. For example, in this case $b=16$ and $5877∕2^{15}\approx 0.1794$.

In case the file had used A-law non-linear PCM, Matlab/Octave could potentially give error messages.

Now, it is suggested to get more familiar with headerless files using Audacity to save a sound file as “raw”. It may be useful to check Appendix B.2 for more details on how the information is organized in binary files. After recording in Audacity, choose Export - Other compressed files (in “type”) as in Figure 1.60, but this time select the header “RAW (header-less)” instead of “WAV (Microsoft)”. For the encoding, select “Signed 16 bit-PCM”, as before, and name the file ’myvoice_raw.wav’. In this case, it would be wiser to use another file extension and name it ’myvoice.raw’, for example. But the purpose of using “wav” is to make clear that the extension by itself cannot guarantee a file format is the expected one.

In this particular example, the file sizes are $29,228$ and $29,184$ for the WAVE and raw formats, respectively. In fact, in spite of a WAVE possibly having a sophisticated structure with several sections (chunks), most of them have a single chunk and one header consisting of the first 44 bytes, which is the difference between the two sizes given that both have the same $29184∕2=14592$ samples of 2 bytes each.

Using the command readwav for the raw file would generate error messages in Matlab/Octave. Based on Appendix B.2.4.0, the following code properly reads the samples:

1fp=fopen('myvoice_raw.wav','rb'); %open for reading in binary 
2x=fread(fp,Inf,'int16'); %read all samples as signed 16-bits 
3fclose(fp);  %close the file

As a sanity check, one can read the samples of the WAVE file, skip its header and compare with the result of readwav with Listing 1.23 on Matlab.

1fp=fopen('myvoice.wav','rb'); %open for reading in binary 
2x=fread(fp,Inf,'int16'); %read all samples as signed 16-bits 
3fclose(fp);  %close the file 
4x(1:22)=[]; %eliminate the 44-bytes header 
5[x2,Fs,wmode,fidx]=readwav('myvoice.wav','r'); % get raw samples 
6b = fidx (7); % num of bits per sample 
7x2=double(x2); %convert integer to double for easier manipulation 
8isequal(x,x2) %result is 1, indicating vectors are identical
  

The advantage of using WAVE is that the header informs $F_s$, $b$, whether its mono or stereo, etc. Also, the WAVE format takes care of endianness (see Appendix B.2.3). Not using readwav, write code in Matlab/Octave to open a WAVE file (with only 1 chunk) and extract $F_s$, $b$ and the samples as integers. This code can be used by Octave users to mimic the option ’s’ (raw) in Matlab’s readwav. It may be useful to read Appendix B.2.5 and use the companion code laps_dump.c, which can be compiled with most C compilers. A short description of the WAVE header is provided at [ url1wav].    $\text{□}$

Application 1.2. Recording sound with Matlab. Colab’s notebook version This application discusses how to record sound directly with Matlab, which has several functions to deal with sound recording and playback. You can check soundsc, audiorecorder, wavplay and wavrecord, for example. Some functions work only on Windows.

Octave has functions such as record and sound and its support to sound is more natural on Linux. There are solutions such as [ url1rec] to record and play sound on Octave running on Windows, but the installation is not trivial.

The following code was used in Matlab to record 5 seconds of one (mono) channel sound at a sampling rate of 11,025 Hz, using 16 bits to represent each sample:

1r=audiorecorder(11025,16,1); %create audiorecorder object 
2record(r,5); %record 5 seconds and store inside object r

One can use play(r) to listen the recorded sound or y = getaudiodata(r, ’int16’) to obtain the samples from the audiorecorder object. However, if one of these commands immediately follows record(r,5), the error can be generated:
??? Cannot retrieve audio data while recording is in progress.
This means the software was still recording when it tried to execute the second command. An alternative is to use recordblocking as in Listing 1.24.

1r=audiorecorder(11025,16,1); %create audiorecorder object 
2recordblocking(r,5); %record 5 seconds and store inside r 
3play(r) %playback the sound 
4y = getaudiodata(r, 'int16'); %extract samples as int16 
5plot(y); %show the graph
  

Note that y in the above example is an array with elements of the type int16, i. e., 2 bytes per sample. This saves storage space when compared to the conventional real numbers stored in double (8 bytes) each, but limits the manipulations. For example, the command soundsc(y,11025) generates an error message if y is int16. In such cases, a conversion as y=double(y) can be used before invoking soundsc (use whos y to check that the storage has quadruplicated).

To write y to a 16-bits per sample WAV file and read it back, use Listing 1.25 but the command double(z)./double(y) shows that the normalization used by wavwrite made z approximately three times y. The Voicebox toolbox ([ url1voi]) has functions readwav and writewav that are smarter than Matlab’s with respect to avoiding the normalization.

1y=[14;50;32767;-32768;14;0]; %example, as column vector 
2writewav(y,11025,'somename.wav','16r') %write as 16-bits 
3z=readwav('somename.wav','r'); %avoid normalization 
4isequal(y,z) %should return true 
5% compare with double representation 
6yd=double(y); %convert from int16 
7yd=yd/max(abs(yd)); %normalize 
8zd=readwav('somename.wav','s'); %with normalization 
9isequal(yd,zd) %should return true
  

Some sound boards allow full-duplex operation, i. e., recording and playing at the same time. Typically the sampling frequency must be the same for both operations. On Windows one can try the wavplay function with the option “async” as exemplified in Listing 1.26.

1Fs = 11025;   %define sampling rate (Hz) 
2fc = 1500; %cosine frequency (Hz) 
3recordingDuration = 1; %duration of recording, in seconds 
4r=audiorecorder(Fs,16,1); 
5while 1 %infinite loop, stop with CTRL+C 
6    recordblocking(r,recordingDuration); 
7    inputSignal  = getaudiodata(r); 
8    p=audioplayer(r); 
9    subplot(211), plot(inputSignal); %graph in time domain 
10    subplot(212), pwelch(double(inputSignal)); %in frequency domain 
11    drawnow %Force the graphics to update immediately inside the loop 
12end
  

Listing 1.26 shows the acquired signal (from the ADC) in both time and frequency domains. In this code, the call to wavplay is non-blocking but samples are lost in the sense that inputSignal is not a perfect cosine. Using a loopback cable, as in Application 1.4, allows to evaluate the system.

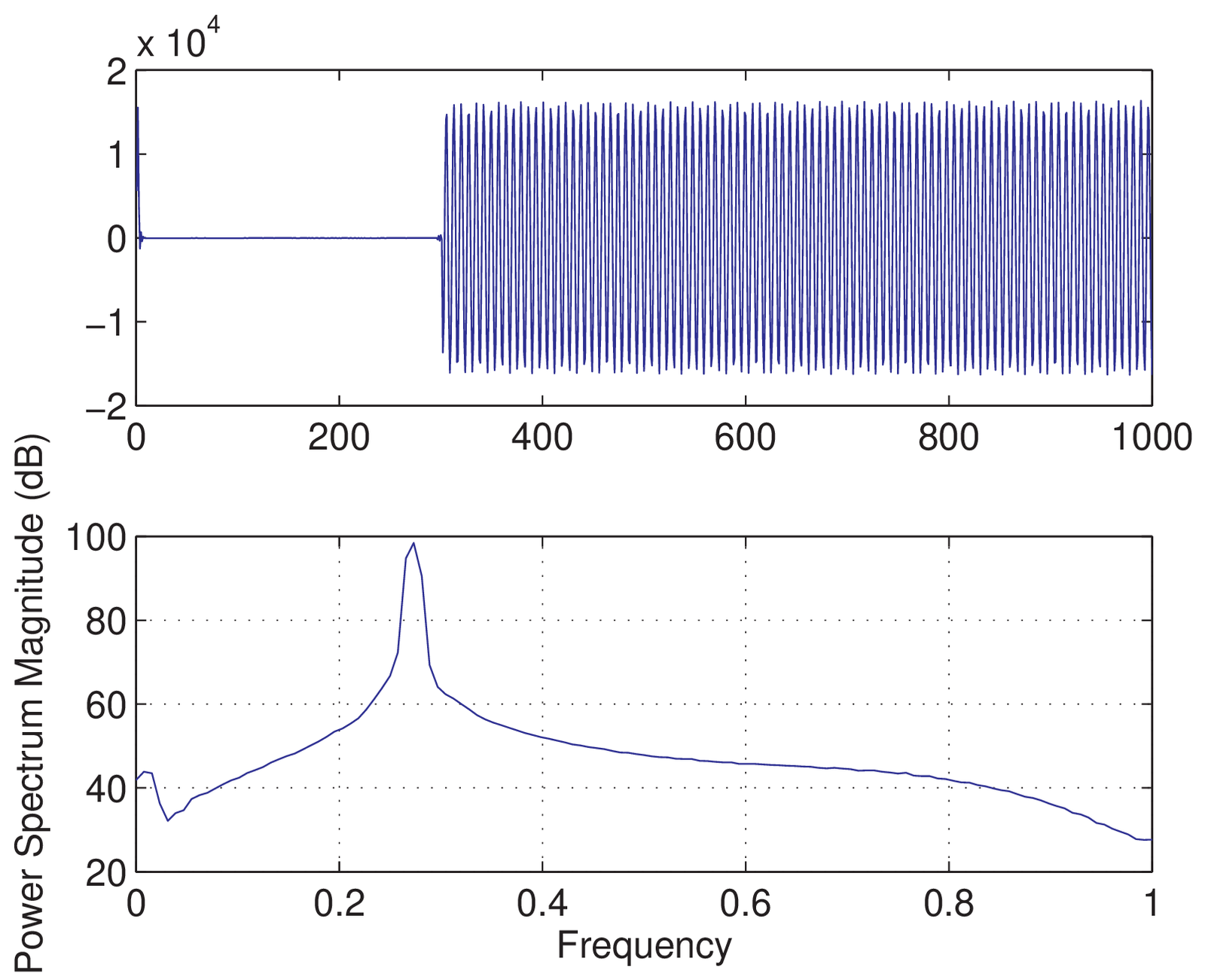
Figure 1.61 was obtained with a loopback. Note from the top plot that approximately 300 samples are a transient and after that one can see the cosine at $f_c=1500$ Hz, which is mapped to $1500∕(F_s∕2)\approx 0.27$ ($F_s=11025$ Hz) in the normalized axis of the bottom plot. In order to get this kind of system running, it is important to reduce the volume (DAC gain) to avoid saturation of the signals.

As an exercise, digitize signals at different sampling frequencies and plot them with the axes properly normalized. Another interesting exploration is to obtain a sound signal inputSignal, digitized at a given rate (e. g., $F_s=11,025$ Hz) and represented by int16. Convert it to double with x=double(inputSignal) in order to easily manipulate the signal and describe what is the result of each of the commands in Listing 1.27.

1fs=22050; %sampling frequency 
2r = audiorecorder(fs, 16, 1);%create audiorecorder object 
3recordblocking(r,5);%record 5 s and store inside object r 
4y = getaudiodata(r,'int16'); %retrieve samples as int16 
5x = double(y); %convert from int16 to double 
6soundsc(x,fs); %play at the sampling frequency 
7soundsc(x,round(fs/2));%play at half of the sampling freq. 
8soundsc(x,2*fs); %play at twice the sampling frequency 
9w=x(1:2:end); %keep only half of the samples 
10soundsc(w,fs); %play at the original sampling frequency 
11z=zeros(2*length(x),1); %vector with twice the size of x 
12z(1:2:end)=x;%copy x into odd elements of z (even are 0) 
13soundsc(z,fs); %play at the original sampling frequency
  

What should be the sampling frequency for vectors w and z in Listing 1.27 to properly listen the audio?   $\text{□}$

Application 1.3. Real time sound processing with Matlab’s DSP System Toolbox. Matlab’s DSP System Toolbox has extended support to interfacing with the sound board. Listing 1.28 provides a simple example that illustrates recording audio.

1exampleNumber=1; %choose 1 (spectrum analyzer) or 2 (digital filter) 
2Fs = 8000;   %define sampling rate (Hz) 
3%create an audio recorder object: 
4microphone = dsp.AudioRecorder('NumChannels',1,'SampleRate',Fs); 
5if exampleNumber==1 
6    specAnalyzer = dsp.SpectrumAnalyzer; %spectrum analyzer object 
7else 
8    [B,A]=butter(4,0.05); %4-th order lowpass Butterworth filter 
9    filterMemory=[]; %initialize the filter's memory 
10    speaker = dsp.AudioPlayer('SampleRate',Fs); %create audio player 
11end 
12disp('Infinite loop, stop with CTRL+C...'); 
13while 1 %infinite loop, stop with CTRL+C 
14    audio = step(microphone); %record audio 
15    if exampleNumber==1 %spectrum analyzer 
16        step(specAnalyzer,audio); %observe audio in frequency domain 
17    else %perform digital filtering 
18        [output,filterMemory]=filter(B,A,audio,filterMemory); 
19        step(speaker, output); %send filtered audio to player 
20    end 
21end
  

Listing 1.28 indicates how to plot the signal in frequency domain or to perform digital filtering. The code may drop samples depending on the computer’s speed. Matlab’s documentation inform how to control the queue and buffer lengths, and also obtain the number of overruns.   $\text{□}$

Application 1.4. Estimating latency using the sound board, Audacity and a loopback cable. The goal here is to practice dealing with digital and analog signals, interfacing Audacity and Matlab/Octave. An audio cable and a single computer (with the sound system working) is all that is needed for many interesting experiments. The user is invited to construct or purchase a cable with the proper connectors for his/her computer. In most cases, a “3.5 mm male to 3.5 mm male audio cable” is the required one, as indicated in Figure 1.62. A single channel (mono) cable may suffice but stereo cables have almost the same cost and can be used in more elaborated experiments.²⁰

The task is to estimate the latency or channel delay, which is the time interval between the signal is transmitted and its arrival at a receiver after passing through a channel. In this specific case, the channel is composed of the sound board hardware (buffers, etc.) and the used device drivers (low-level software that interfaces with the hardware) and application software (Audacity in this case). In sound processing, latency is especially important when overdubbing, i. e., recording a track while playing back others. A detailed description of testing the latency with Audacity can be found at [ url1lat].

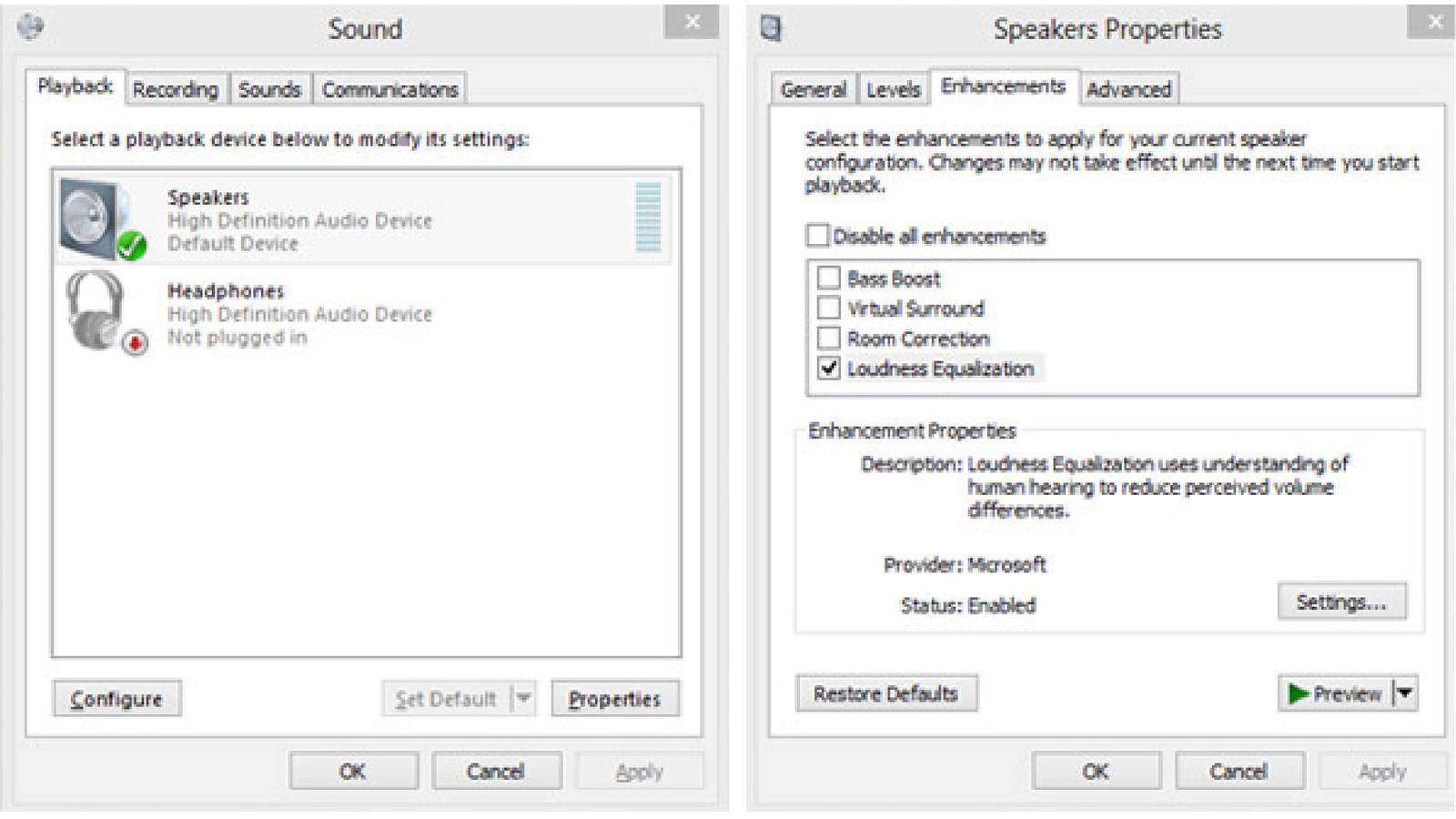
To have a better control of the sound board, it is important to disable all special effects and enhancements for both recording and playback devices, such as automatic gain control for the input ADC signal. Figure 1.63 provides screenshots from Windows but users of other operating systems should be able to find how to choose the best sound options.

After making sure the best configuration for your sound system was chosen, the task now is to generate some samples of a periodic train of impulses. Instead of impulses, the Audacity menu “Generate - Click Track” provides a dialog window with other options. But here the suggestion is to use Matlab/Octave and create a signal with N discrete-time impulses $\delta [n]$. Note that the analog signal corresponding to $\delta [n]$ will never be the theoretical continuous-time $\delta (t)$. For example, assuming zero-order reconstruction (see Figure 1.35), the amplitude of $\delta [n]$ would be held constant during the whole sampling interval $T_s$. Aware of this limitation, Listing 1.29 generates a train of $N$ discrete-time impulses and saves it to a WAVE file.

1Fs = 44100; %sampling frequency 
2Ts = 1/Fs; %sampling period 
3Timpulses = 0.25; %interval between impules in seconds 
4L=floor(Timpulses/Ts); %number of samples between impulses 
5N = 4; %number of impulses 
6impulseTrain=zeros(N*L,1); %allocate space with zeros 
7b=16; %number of bits per sample 
8amplitude = 2^(b-1)-1; %impulse amplitude, max signed int 
9impulseTrain(1:L:end)=amplitude; %generate impulses 
10writewav(impulseTrain,Fs,'impulses.wav','16r') %save WAVE RIFF
  

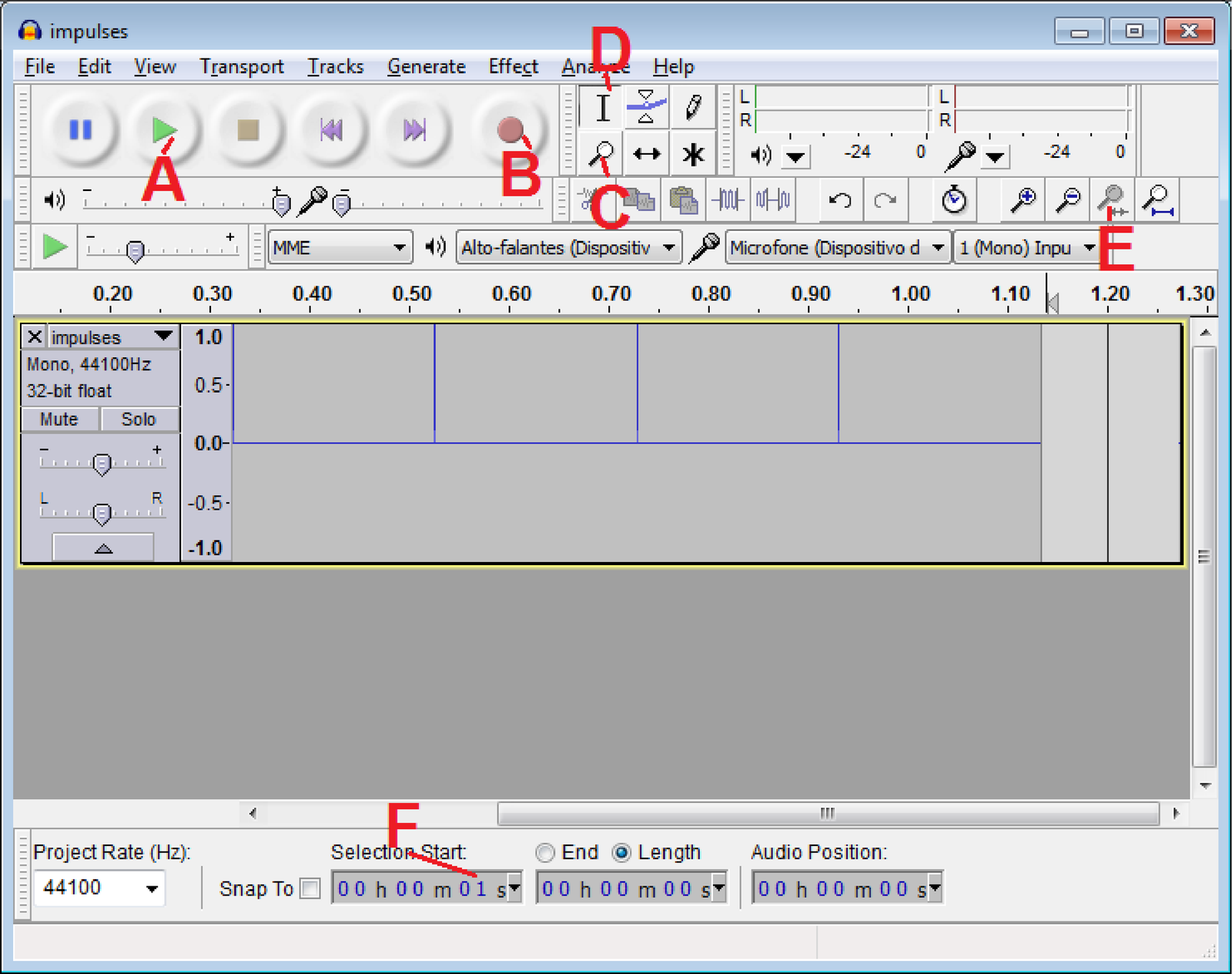
Opening the generated file with Audacity should lead to Figure 1.64. Note the amplitudes have been normalized and the first impulse barely appears. In this case, as indicated by letter F in Figure 1.64, the selection region starts approximately at 1 s. The interface is friendly and the letters C and D indicate how to switch between zooming the signal and enabling the cursor, respectively. After a segment is selected, letter E indicates how to easily zoom it to fit the selection. Instead of seconds (in letter F), it is sometimes convenient to use “samples”. Using the play button indicated with letter A plays the file.

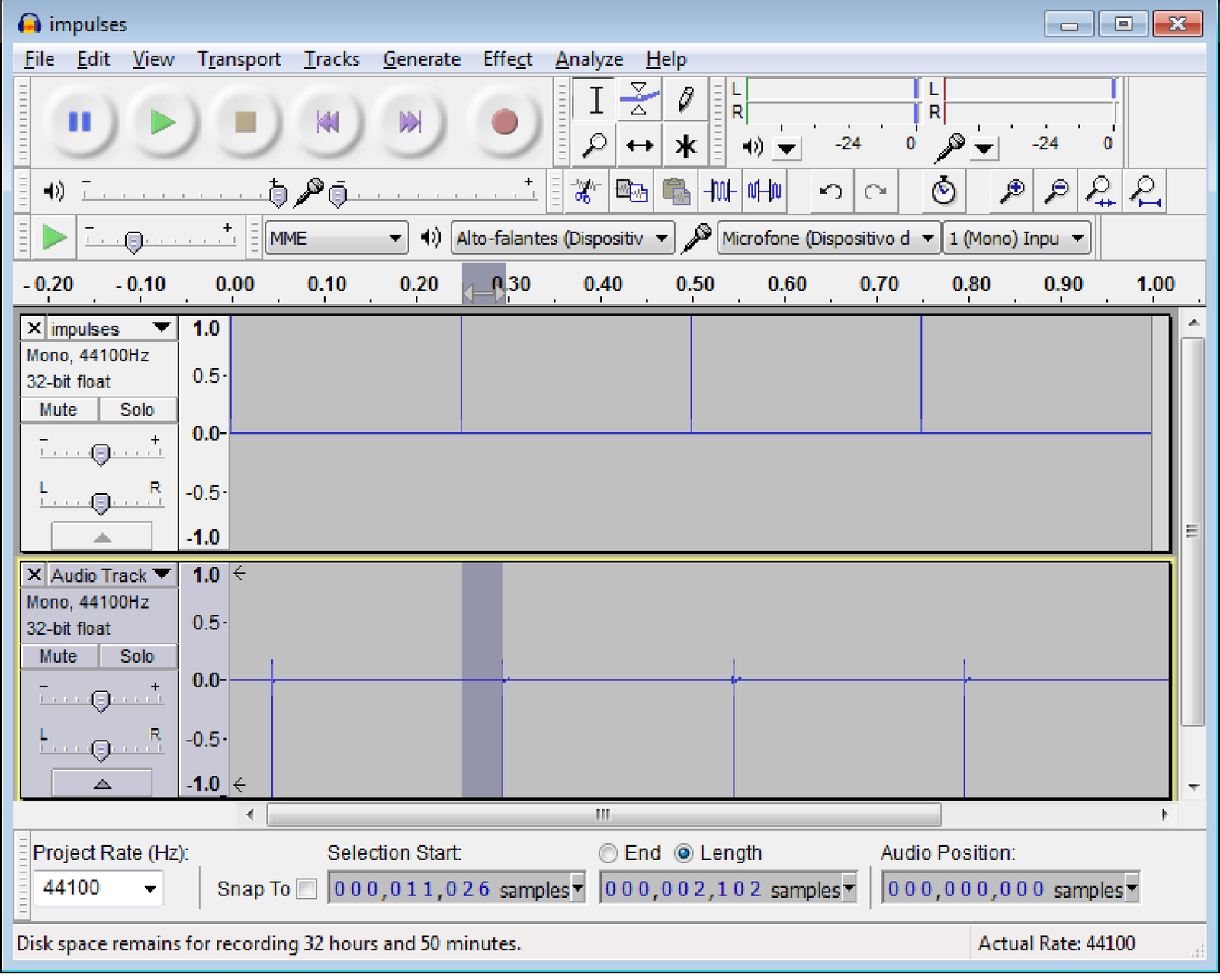
At this point, a feature of Audacity that is useful for overdubbing can be used to simultaneously activate the DAC and ADC: when recording, Audacity also plays all the signals that are “open” (in this case, the “impulses” signal). With the audio cable connected in loopback, start recording (and playback) simply using button (letter B), stopping it after a second. The final situation should be similar to Figure 1.65.

From the code used to generate ’impulses.wav’ it can be seen that the impulses are separated by $F_s∕4=11025$ samples (the first one is at $n=1$, the second at $n=11026$ and so on). This information was used to impose the start selection (letter F in Figure 1.64) at sample 11,026 in Figure 1.65 (it is irrelevant here, but recall that the first index in Matlab/Octave is 1 but 0 in Audacity). The end of the selection was located approximately at the start of the second impulse of the recorded signal (bottom plot, identified as “Audio Track”). In this case, the number of samples of this selection indicate that the latency was approximately $2102\times T_s\approx 47.66$ ms.

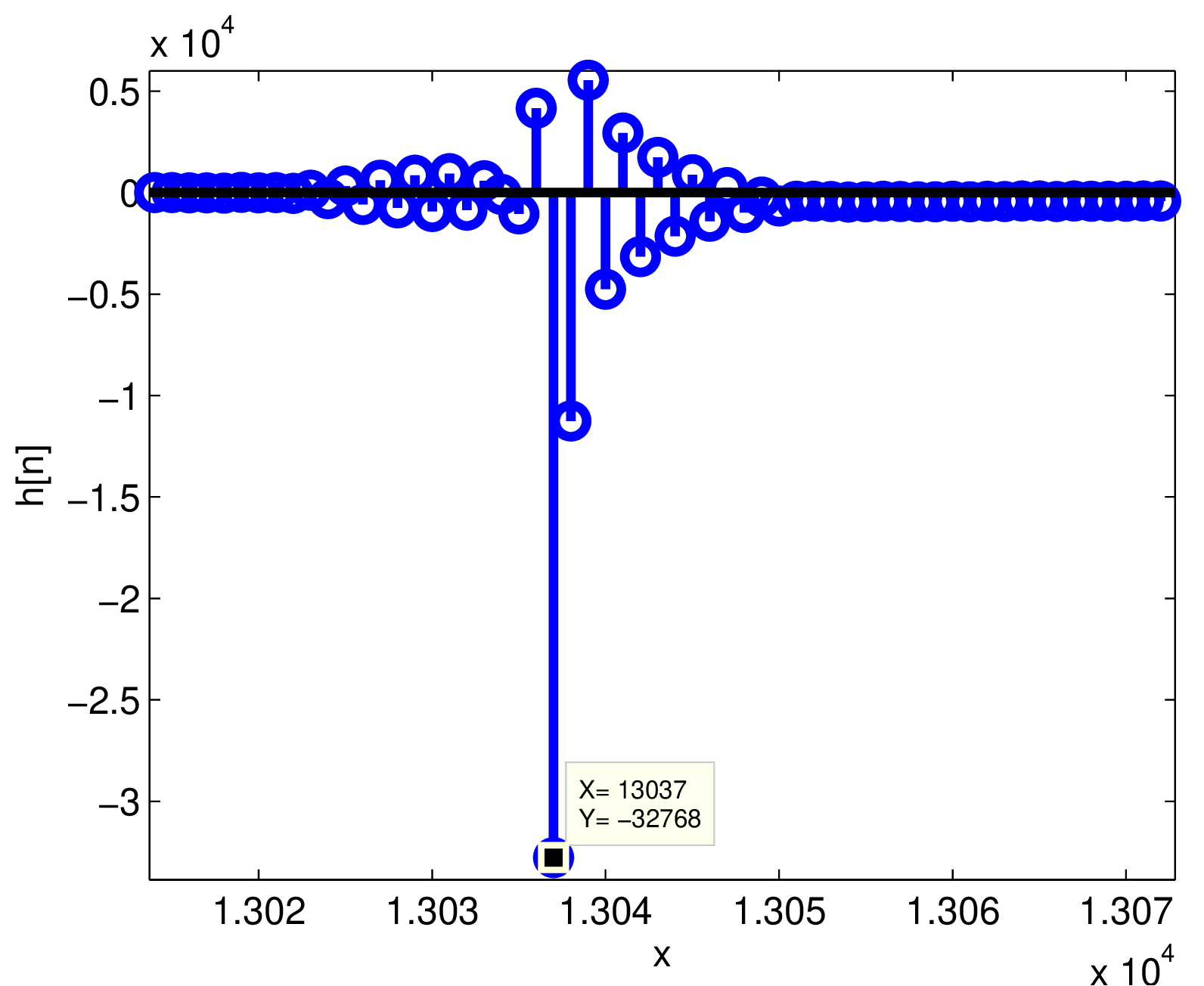
At this point it may be useful to export the recorded signal as a WAVE file to be read in Matlab/Octave. First, you can close the window with the “impulses” signal (otherwise Audacity will ask if the two files should be merged) and use the “Export” menu. Assuming the output file name was impulseResponses.wav, the command h=readwav(’impulseResponses.wav’) can be used to generate the zoom of the second impulse response in Figure 1.66. The concept of impulse response is very important, as discussed in Chapter 3.

Because the maximum absolute amplitude occurs at $n=13037$ in Figure 1.66 and the corresponding impulse is located at $n=11026$, another estimate of the latency is $(13037-11026)T_s\approx 45.6$ ms. A detail is that for creating Figure 1.66, the ‘s’ option of Matlab’s readwav was used to avoid normalization and, consequently, the minimum signal value is $-2^{b-1}=-32768$ not $-1$.    $\text{□}$

Application 1.5. PC sound board quantizer. Given a system with an ADC, typically one has to know beforehand or conduct measurements to obtain the quantizer step size $\mathrm{\Delta }$. This is the case when using a personal computer (PC) sound board. For a sound board, the value of $\mathrm{\Delta }$ depends if the signal was acquired using the microphone input or the line-in input of the sound board. The microphone interface is designed for signals with peak value of $X_{\mathrm{\text{max}}}=10$ to 100 mV while the peak for the line-in is typically 0.2 to 2 V. Note that the voltage ranges of line inputs and microphones vary from card to card. See more details in [ url1pcs]. For the sake of this discussion, one can assume a dynamic range of $[-100,100]$ mV and a ADC of 8 bits per sample, such that $\mathrm{\Delta }=200∕(2^8-1)\approx 0.78$ mV. The following example illustrates how to approximately recover the analog signal for visualization purposes. Assume the digital dynamic range is [0, 255] and the digital samples are $D=[13,126,3,34,254]$. If one simply uses stem(D), there is no information about time and amplitude. Listing 1.30 shows the necessary normalizations to visualize the abscissa in seconds and the ordinate in volts, which in this case corresponds to A=1000*[-89.70, -1.56, -97.50, -73.32, 98.28].

1D=[13 126 3 34 254]; %signal as 8-bits unsigned [0, 255] 
2n=[0:4]; %sample instants in the digital domain 
3Fs=8000; %sampling frequency 
4delta=0.78e-3; %step size in Volts 
5A=(D-128)*delta; %subtract offset=128 and normalize by delta 
6Ts=1/Fs; %sampling interval in seconds 
7time=n*Ts; %normalize abscissa 
8stem(time,A); %compare with stem(n,D) 
9xlabel('time (s)'); ylabel('amplitude (V)');
  

Now assume a PC computer with a sound board that uses a 16 bits ADC and supports at its input a dynamic range of $-185$ to $185$ mV. The quantizer is similar to the one depicted in Figure 1.48, but the quantization step should be $\mathrm{\Delta }=2\times 185\times 10^{-3}∕2^{16}\approx 5.6$ $\mu$V. It is assumed here that $\mathrm{\Delta }=5.6$ $\mu$V and the quantizer is uniform from $-2^{15}\mathrm{\Delta }$ to $(2^{15}-1)\mathrm{\Delta }$. In this case, the $M=65,536=2^{16}$ levels are organized as 32,767 positive levels, 32,768 negative levels and one level representing zero. The assumed coding scheme is the offset code of Table 1.8 with 32,768 as the offset. Hence, the smallest value $-2^{15}\mathrm{\Delta }$ is mapped to the 16-bits codeword “0000 0000 0000 0000”, $(-2^{15}+1)\mathrm{\Delta }$ to “0000 0000 0000 0001” and so on, with $(2^{15}-1)\mathrm{\Delta }$ being coded as “1111 1111 1111 1111”.

If at a specific time $t_0$ the ADC input is $x(t_0)=x=0.003$ V, the ADC output is $x_i=536$, which corresponds to $x_q=0.0030016$ V and leads to a quantization error $e=x-x_q\approx -1.6\times 10^{-6}$ V. These results can be obtained in Matlab/Octave with

1delta=5.6e-6, b=16 %define parameters for the quantizer 
2format long %see numbers with many decimals 
3x=3e-3; [xq,xi]=ak_quantizer(x,delta,b), error=x-xq

Based on similar reasoning, calculate the outputs $x_i$ of the quantizer, their respective $x_q$ values and the quantization error for $x\in \{-300,-100,0,20,180\}$ mV.

If you have access to an oscilloscope and a function generator, try to estimate the value of $\mathrm{\Delta }$ of your sound board, paying attention to the fact that some software/hardware combination use automatic gain control (AGC). You probably need to disable AGC to better control the acquisition.

It is not trivial, but if you want to learn more about your sound board, try to evaluate its performance according to the procedure described at [ url1bau].    $\text{□}$

Application 1.6. Using rat in Matlab/Octave to find the period of discrete-time sinusoids. The Matlab/Octave function rat for rational fraction approximation can be used for finding $m$ and $N$. But care must be exercised because rat approximates the input argument within a given tolerance. The code below illustrates how this function can be used to obtain $m$ and $N$:

1w=3*pi/5 %define some angular frequency (rad) 
2[m,N]=rat(w/(2*pi)) %find m and N

In this case, the result is m=3, N=10, as expected. However, note that w=0.2,[m,N]=rat(w/(2*pi)) returns m=113, N=3550, which is not precise (recall that if $\mathrm{\Omega }=0.2$ the sinusoid is non-periodic). Modifying the previous command to use a smaller tolerance w=0.2,[m,N]=rat(w/(2*pi),1e-300) gives much larger values for m,N, which clearly indicates that the user must be aware that rat uses approximations. Make sure you can generate discrete-time sinusoids with distinct values of $m$ and $N$ and understand the roles played by these two values.    $\text{□}$

Application 1.7. Power of the sum of two signals. Assume a signal $z[n]=x[n]+y[n]$ is generated by summing two real signals (similar result can be obtained for complex-valued signals) $x[n]$ and $y[n]$ with power $P_x$ and $P_y$. The question is: What is the condition for having $P_z=P_x+P_y$?

Assuming the two signals are random and using expected values (a similar result would hold for deterministic signals):

If $X$ and $Y$ are uncorrelated, i. e., $𝔼[XY]=𝔼[X]𝔼[Y]$ and at least one signal is zero-mean, Eq. (1.73) simplifies to

This is a useful result for analyzing communication channels that model the noise as additive. These models assume the noise is uncorrelated to the transmitted signal and Eq. (1.74) applies.   $\text{□}$

Application 1.8. Estimate the PDF of speech signals. Via a normalized histogram, estimate the PDF of a speech signal with a long duration. After this estimation, you should convince yourself that uniform quantizers are not adequate for speech signals. In fact, when using a non-linear quantizer based on the A-law or $\mu$-law, it is possible to use only 8 bits to achieve the subjective quality of a linear PCM with 12 bits. Observe whether or not your histogram approaches a Laplacian density, as suggested by previous research in speech coding.    $\text{□}$

Application 1.9. A simple application of correlation analysis. A company produces three distinct beauty creams: A, B and C. The task is the analysis of correlation in three databases, one for each product. The contents of each database can be represented by two vectors $\mathbf{\text{x}}$ and $\mathbf{\text{y}}$, with 1,000 elements each. Vector $\mathbf{\text{x}}$ informs the age of the consumer and $\mathbf{\text{y}}$ the number of his/her purchases of the respective cream (A, B or C) during one year, respectively. Figure 1.67 depicts scatter plots corresponding to each product.

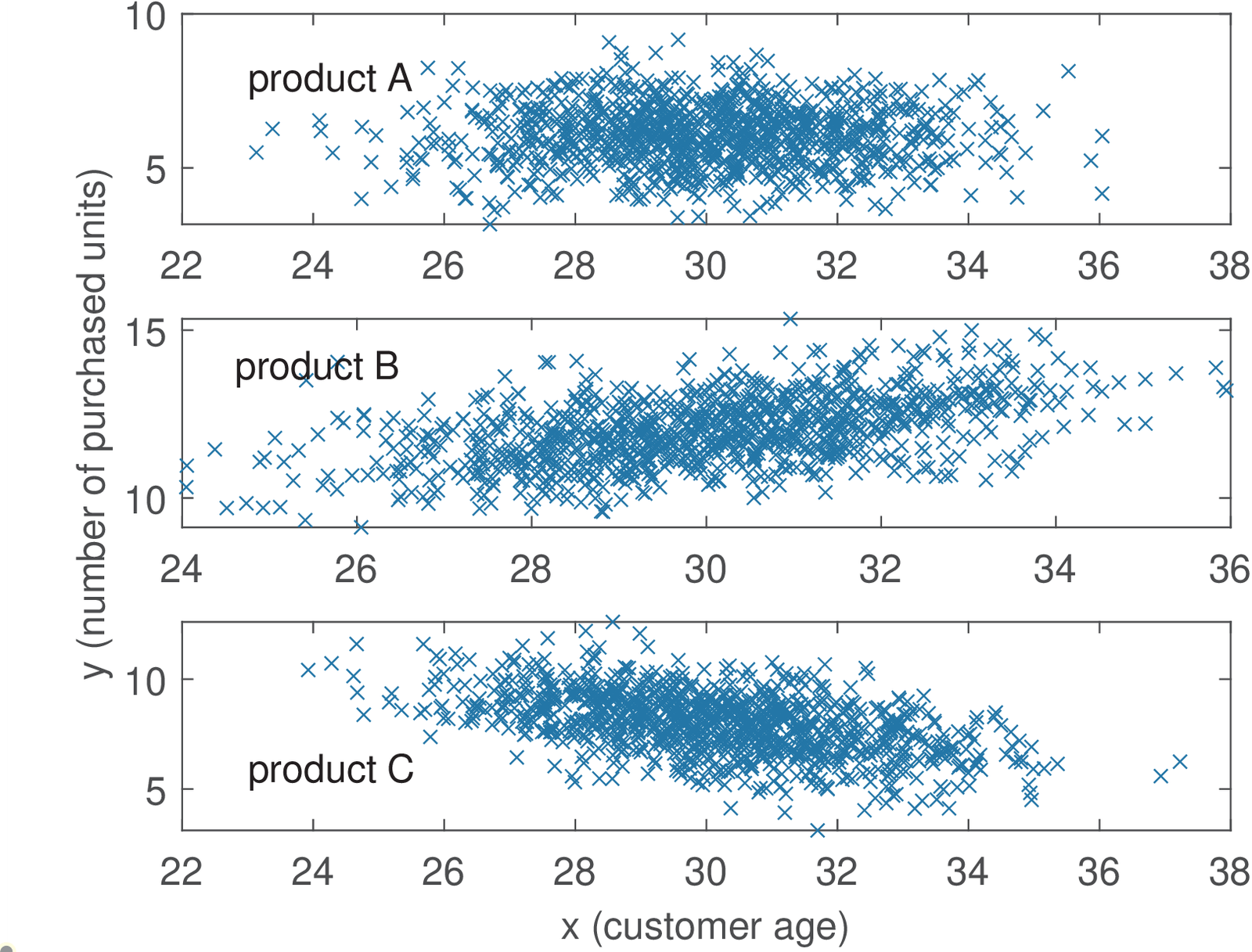
The empirical (the one calculated from the available data) covariance matrices and means were approximately the following: ${\mathbf{\text{C}}}_a=\left[\begin{array}{cc}\hfill 4.08\hfill & \hfill -0.002\hfill \\ \hfill \hfill \\ \hfill \hfill \\ \hfill -0.002\hfill & \hfill 0.98\hfill \end{array}\right]$and ${\mu }_a=[30.0,6.05]$, ${\mathbf{\text{C}}}_b=\left[\begin{array}{cc}\hfill 4.00\hfill & \hfill 0.99\hfill \\ \hfill \hfill \\ \hfill \hfill \\ \hfill 0.99\hfill & \hfill 1.00\hfill \end{array}\right]$and ${\mu }_b=[30.1,12.0]$, ${\mathbf{\text{C}}}_c=\left[\begin{array}{cc}\hfill 4.16\hfill & \hfill -1.46\hfill \\ \hfill \hfill \\ \hfill \hfill \\ \hfill -1.46\hfill & \hfill 2.02\hfill \end{array}\right]$and ${\mu }_c=[30.13,7.99]$. The correlation coefficients are ${\rho }_a=-0.0011$, ${\rho }_b=0.4924$ and ${\rho }_c=-0.5031$.

The plots and correlation coefficients indicate that when age increases, the sales of product B also increases (positive correlation). In contrast, the negative correlation of ${\rho }_b$ indicates that the sales of product C decreases among older people. The sales of product A seem uncorrelated with age. The script figs_signals_correlationcoeff.m allows to study how the data and figures were created. Your task is to learn how to generate two-dimensional Gaussians with arbitrary covariance matrices.

Note that the correlation analysis was performed observing each product sales individually. You can assume the existence of a unique database, where each entry has four fields: age, sales of A, B and C. What kind of analysis do you foresee? For example, one could try a marketing campaign that combines two product if their sales are correlated. Or even use data mining tools to extract association rules that indicate how to organize the marketing.    $\text{□}$

Application 1.10. Playing with the autocorrelation function of white noise and sinusoids. Using randn in Matlab/Octave, generate a vector corresponding to a realization of a WGN process (see Example 1.50): x=randn(1,1000). Check whether or not it is Gaussian by estimating the FDP (use hist). Plot its autocorrelation with the proper axes. Generate a new signal that is uniformly distributed: y=rand(1,1000)-0.5; and plot the same graphs as for the Gaussian signal. What does it happen with the autocorrelation if you add a DC level (add a constant to x and y)? And what if you multiply by a number (a “gain”)? Generate a cosine T=0.01; t=0:T:10-T; z=cos(2*pi*10*t); of 10 Hz with a sampling frequency of 100 Hz. Take a look at the autocorrelation for lags from $m=-30,\dots ,30$ with [c,lags]=xcorr(z,30,’biased’);plot(lags,c). Compare this last plot with a zoom of the cosine: plot(z(1:30)). Note that they have the same period. In fact, an autocorrelation $R$ of $x$ incorporates all the periodicity that is found in $x$ as indicated by Eq. (1.58). Make sure you can use Eq. (1.58) to predict the plots you obtain with xcorr when the signal is a sinusoid.    $\text{□}$

Application 1.11. Using autocorrelation to estimate the cycle of sunspot activity. The international sunspot number (also known as the Wolfer number) is a quantity that simultaneously measures the number and size of sunspots. A sunspot is a region on the Sun’s surface that is visible as dark spots. The number of sunspots correlates with the intensity of solar radiation: more sunspots means a brighter sun. This number has been collected and tabulated by researchers for around 300 years. They have found that sunspot activity is cyclical and reaches its maximum around every 9.5 to 11 years (in average, 10.4883 years).²¹ The autocorrelation can provide such estimate as indicated by the script below. Note that we are not interested in $R(0)$, which is always the maximum value of $R(\tau )$. The lag of the largest absolute value of $R(\tau )$ other than $R(0)$ indicates the signal fundamental period. Because theoretically no other value can be larger than $R(0)$, the task of automatically finding the second peak (not the second largest sample), which is the one of interest, is not trivial. The code snippet below simply (not automatically) indicates the position of the second peak for the sunspot data.

1load sunspot.dat; %the data file 
2year=sunspot(:,1); %first column 
3wolfer=sunspot(:,2); %second column 
4%plot(year,wolfer); title('Sunspot Data') %plot raw data 
5x=wolfer-mean(wolfer); %remove mean 
6[R,lag]=xcorr(x); %calculate autocorrelation 
7plot(lag,R); hold on; 
8index=find(lag==11); %we know the 2nd peak is lag=11 
9plot(lag(index),R(index),'r.', 'MarkerSize',25); 
10text(lag(index)+10,R(index),['2nd peak at lag=11']);
  

Figure 1.68 shows the graph generated by the companion script figs_signals_correlation.m. It complements the previous code snippet, showing how to extract the second peak automatically (this can be useful in other applications of the ACF). Your task is to study this code and get prepared to work with “pitch” estimation in Application 1.12.

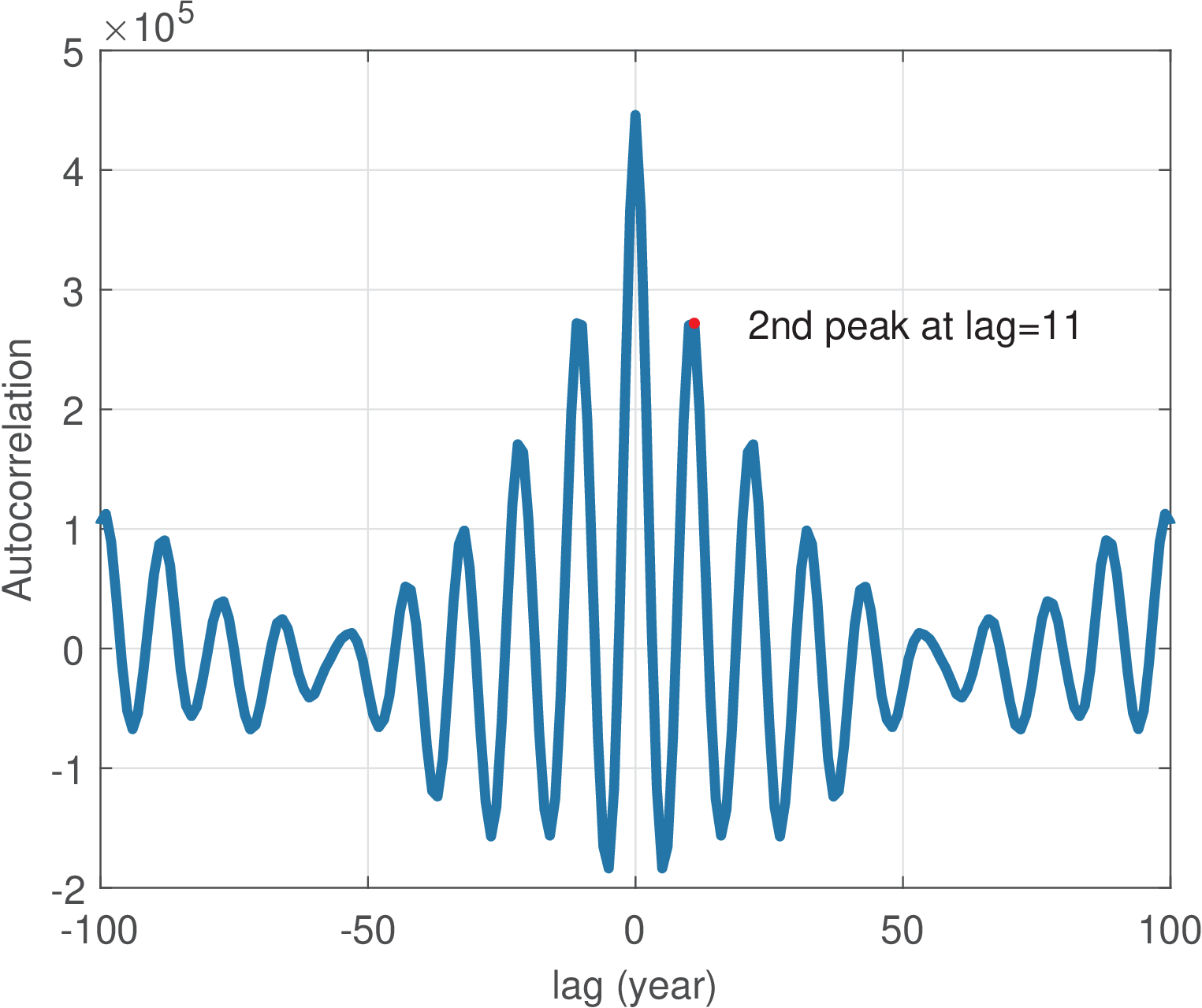
An important aspect of the sunspot task is the interpretation of $R(\tau )$. As discussed, when the autocorrelation has a peak, it is an indication of high similarity, i. e., periodicity. In the sunspot application, the interval between two lags was one year. If the ACF is obtained from a signal sampled at $F_s$ Hz, this interval between lags is the sampling period $T_s=1∕F_s$ and it is relatively easy to normalize the lag axis. The next example illustrates the procedure.    $\text{□}$

Application 1.12. Using autocorrelation to estimate the “pitch”. This application studies a procedure to record speech, estimate the average fundamental frequency $F0$ (also erroneously but commonly called pitch) via autocorrelation and play a sinusoid with a frequency proportional to $F0$.

One can estimate the fundamental frequency of a speech signal by looking for a peak in the delay interval corresponding to the normal pitch range in speech.²² The following script illustrates the procedure.

1Fs=44100; %sampling frequency 
2Ts=1/Fs; %sampling interval 
3minF0Frequency=80; %minimum F0 frequency in Hz 
4maxF0Frequency=300; %minimum F0 frequency in Hz 
5minF0Period = 1/minF0Frequency; %correponding F0 (sec) 
6maxF0Period = 1/maxF0Frequency; %correponding F0 (sec) 
7Nbegin=round(maxF0Period/Ts);%number of lags for max freq. 
8Nend=round(minF0Period/Ts); %number of lags for min freq. 
9if 0 %record sound or test with 300 Hz cosine 
10    r = audiorecorder(Fs, 16, 1);%object audiorecorder 
11    disp('Started recording. Say a vowel a, e, i, o or u') 
12    recordblocking(r,2);%record 2 s and store in object r 
13    disp('finished recording'); 
14    y=double(getaudiodata(r, 'int16'));%get recorded data 
15else %test with a cosine 
16    y=cos(2*pi*300*[0:2*Fs-1]*Ts); %300 Hz, duration 2 secs 
17end 
18subplot(211); plot(Ts*[0:length(y)-1],y); 
19xlabel('time (s)'); ylabel('Signal y(t)') 
20[R,lags]=xcorr(y,Nend,'biased'); %ACF with max lag Nend 
21subplot(212); %autocorrelation with normalized abscissa 
22plot(lags*Ts,R); xlabel('lag (s)'); 
23ylabel('Autocorrelation of y(t)') 
24firstIndex = find(lags==Nbegin); %find index of lag 
25Rpartial = R(firstIndex:end); %just the region of interest 
26[Rmax, relative_index_max]=max(Rpartial); 
27%Rpartial was just part of R, so recalculate the index: 
28index_max = firstIndex - 1 + relative_index_max; 
29lag_max = lags(index_max); %get lag corresponding to index 
30hold on; %show the point: 
31plot(lag_max*Ts,Rmax,'xr','markersize',20); 
32F0 = 1/(lag_max*Ts); %estimated F0 frequency (Hz) 
33fprintf('Rmax=%g lag_max=%g T=%g (s) Freq.=%g Hz\n',... 
34    Rmax,lag_max,lag_max*Ts,F0); 
35t=0:Ts:2; soundsc(cos(2*pi*3*F0*t),Fs); %play freq. 3*F0
  

Figure 1.69 was generated using the previous script with the signal $y(t)$ consisting of a cosine of 300 Hz instead of digitized speech (simply change the logical condition of the “if”).

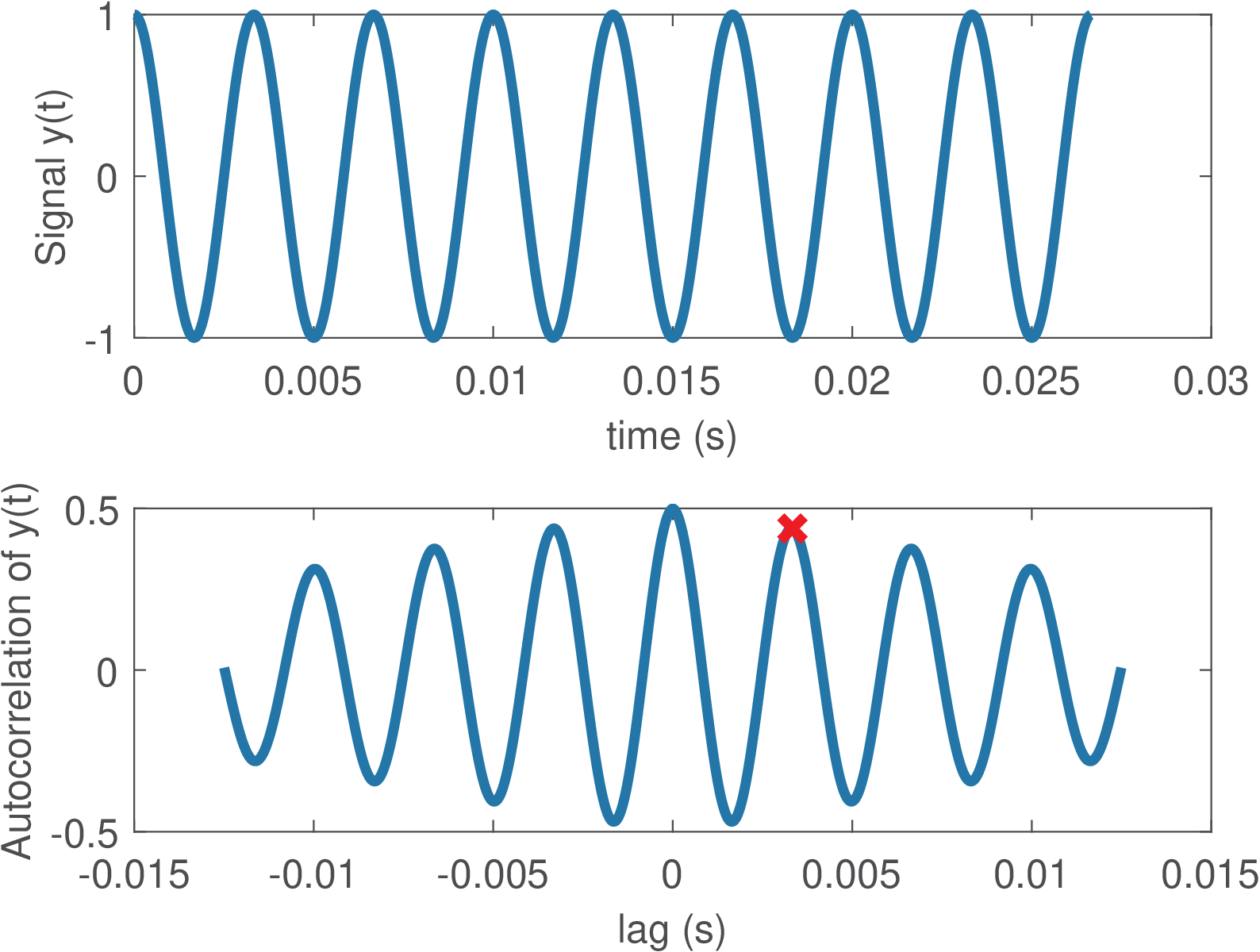
The code outputs the following results:
Rmax=0.49913 lag_max=147 T=0.00333333 (sec) Frequency=300 Hz
Note that the autocorrelation was normalized xcorr(y,Nend,’biased’), which led to $R(0)\approx 0.5$ Watts, coinciding with the sinusoid power $A^2∕2$, where $A=1$ V is the sinusoid amplitude.

As commonly done, in spite of dealing with discrete-time signals, the graphs assume the signals are approximating a continuous-time signal and ACF. Hence, the abscissa is $t$, not $n$.

Some PC sound boards heavily attenuate the signals around 100 Hz. Therefore, the last command multiplies the estimated $F0$ by 3, to provide a more audible tone. Modify the last line of the code to use $F0$ instead of $3F0$ and observe the result of varying F0 with your own voice. Then try to improve the code to create your own F0 estimation algorithm. Find on the Web a Matlab/Octave F0 (or pitch) estimation algorithm to be the baseline (there is one at [ url1pit]) and compare it with your code. Use the same input files for a fair comparison and superimpose the pitch tracks to spectrograms to better compare them. If you enjoy speech processing, try to get familiar with Praat [ url1pra] and similar softwares and compare their F0 estimations with yours.    $\text{□}$

Application 1.13. Using cross-correlation for synchronization of two signals or time-alignment. Assume a discrete-time signal $x[n]$ is transmitted through a communication channel and the receiver obtains a delayed and distorted version $y[n]$. The task is to estimate the delay imposed by the channel. The transmitter does not “stamp” the time when the transmission starts, but uses a predefined preamble sequence $p[n]$ that is known by the receiver. The receiver will then guess the beginning of the transmitted message by searching for the preamble sequence in $y[n]$ via cross-correlation. Before trying an example that pretends to be realistic, some simple manipulations can clarify the procedure.

Assume we want to align the signal $x[n]=\delta [n]+2\delta [n-1]+3\delta [n-2]$ with $y[n]=3\delta [n]+2\delta [n-1]+\delta [n-2]+\delta [n-3]+2\delta [n-4]+2\delta [n-5]$. Intuitively, the signal $x[n-3]$ is a good match to $y[n]$. Alternatively, $y[n+3]$ matches $x[n]$. The Matlab/Octave command xcorr(x,y) for cross-correlation can help finding the best lag $L$ such that $x[n+L]$ matches $y[n]$. The procedure is illustrated below:

1x=1:3; %some signal 
2y=[(3:-1:1) x]; %the other signal 
3[c,lags]=xcorr(x,y); %find cross-correlation 
4max(c) %show the maximum cross-correlation value 
5L = lags(find(c==max(c))) %lag for max cross-correlation 
6stem(lags,c); %plot 
7xlabel('lag (samples)'); ylabel('cross-correlation')
  

The result is $L=-3$. If the order is swapped to xcorr(y,x) as below, the result is $L=3$.

1[c,lags]=xcorr(y,x); 
2max(c) %show the maximum cross-correlation value 
3maxlag=lags(find(c==max(c))) %max cross-correlation y,x lag

It should be noticed that the cross-correlation is far from perfect with respect to capturing similarity between waveforms. For example, if $y[n]$ is changed to y=[(4:-1:1) x], the previous commands would indicate the best lag as $L=1$. The reader is invited to play with simple signals and find more evidence of this limitation. As a rule of thumb, the cross-correlation will work well if one of the signals is a delayed version of the other, without significant distortion. However, in situations such as reverberant rooms where one of the signals is composed by a sum of multi-path (with distinct delays) versions of the other signal, more sophisticated techniques should be used.

Another aspect is that, in some applications, the best similarity measure is the absolute value of the cross-correlation (i. e., L = lags(find(abs(c)==max(abs(c)))) instead of L = lags(find(c==max(c)))). For example, this is the case when $x[n]$ can be compared either to $y[n]$ or $-y[n]$.

Listing 1.34 illustrates the delay estimation between two signals $x[n]$ and $y[n]$. The vector y, representing $y[n]$, is obtained by delaying x and adding Gaussian noise to have a given SNR.

1Fs=8000; %sampling frequency 
2Ts=1/Fs; %sampling interval 
3N=1.5*Fs; %1.5 seconds 
4t=[0:N-1]*Ts; 
5if 1 
6    x = rand(1,N)-0.5; %zero mean uniformly distributed 
7else 
8    x = cos(2*pi*100*t); %cosine 
9end 
10delayInSamples=2000; 
11timeDelay = delayInSamples*Ts %delay in seconds 
12y=[zeros(1,delayInSamples) x(1:end-delayInSamples)]; 
13SNRdb=10; %specified SNR 
14signalPower=mean(x.^2); 
15noisePower=signalPower/(10^(SNRdb/10)); 
16noise=sqrt(noisePower)*randn(size(y)); 
17y=y+noise; 
18subplot(211); plot(t,x,t,y); 
19[c,lags]=xcorr(x,y); %find crosscorrelation 
20subplot(212); plot(lags*Ts,c); 
21%find the lag for maximum absolute crosscorrelation: 
22L = lags(find(abs(c)==max(abs(c)))); 
23estimatedTimeDelay = L*Ts
  

Figure 1.70 illustrates the result of running the previous code. The random signals have zero mean and uniformly distributed samples. The estimated delay via xcorr(x,y) was -0.25 s. The negative value indicates that x is advanced with respect to y. The command xcorr(y,x) would lead to a positive delay of 0.25 s.

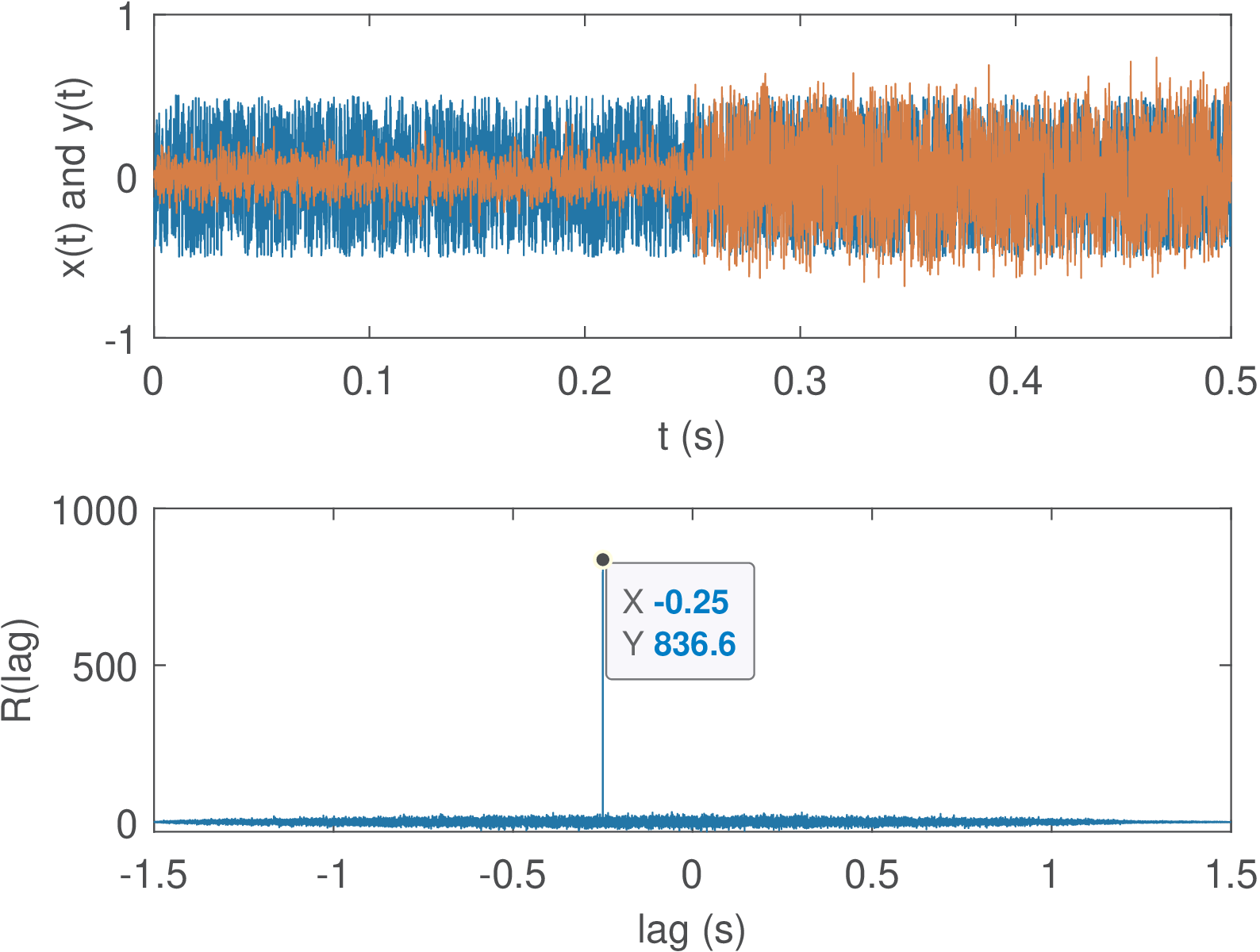
After running the code as it is, observe what happens if x=rand(1,N), i. e., use a signal with a mean different than zero (0.5, in this case). In this case, the correlation is affected in a way that the peak indicating the delay is less pronounced. Another test is to use a cosine (modify the if) with delayInSamples assuming a small value with respect to the total length N of the vectors. The estimation can fail, indicating the delay to be zero. Another parameter to play with is the SNR. Use values smaller than 10 dB to visualize how the correlation can be useful even with negative SNR.

It is important to address another issue: comparing vectors of different length. Assume two signals $x[n]$ and $y[n]$ should be aligned in time and then compared sample-by-sample, for example to calculate the error $x[n]-y[n]$. There is a small problem for Matlab/Octave if the vectors have a different length. Assuming that xcorr(x,y) indicated the best lag is positive ($L>0$), an useful post-processing for comparing $x[n]$ and $y[n]$ is to delete samples of $x[n]$. If $L$ is negative, the first samples of $y[n]$ can be deleted. Listing 1.35 illustrates the operation and makes sure that the vectors representing the signals have the same length.

1x=[1 -2 3 4 5 -1]; %some signal 
2y=[3 1 -2 -2 1 -4 -3 -5 -10]; %the other signal 
3[c,lags]=xcorr(x,y); %find crosscorrelation 
4L = lags(find(abs(c)==max(abs(c)))); %lag for the maximum 
5if L>0 
6  x(1:L)=[]; %delete first L samples from x 
7else 
8  y(1:-L)=[]; %delete first L samples from y 
9end 
10if length(x) > length(y) %make sure lengths are the same 
11  x=x(1:length(y)); 
12else 
13  y=y(1:length(x)); 
14end 
15plot(x-y); title('error between aligned x and y');
  

Elaborate and execute the following experiment: record two utterances of the same word, storing the first in a vector x and the second in y. Align the two signals via cross-correlation and calculate the mean-squared error (MSE) between them (for the MSE calculation it may be necessary to have vectors of the same length, as discussed).    $\text{□}$