Relating spectra of digital and analog frequencies

2.6 Relating spectra of digital and analog frequencies

If $x [n]$ is obtained by sampling $x (t)$ , it is convenient to relate their spectra. This is a followup of Section 1.8. Recall from Eq. (1.36) that $ω = Ω F_{s}$ . Hence, $F_{s}$ can be used to relate the abscissas of graphs of $X (e^{j Ω})$ and $X (ω)$ . But the periodicity of $X (e^{j Ω})$ should be taken into account as follows.

After a sampling frequency $F_{s}$ is specified (e. g., $F_{s} = 8$ kHz), the value $F_{s} ∕ 2$ represents the frequency $f$ that will be mapped to the angle $π$ rad and its multiples in $2 π$ . This can be seen by

Ω = ω ∕ F_{s} = 2 πf ∕ F_{s} = 2 π 4000 ∕ 8000 = π .

(2.36)

In discrete-time (or “digital”) signal processing, the value of $F_{s} ∕ 2$ is called Nyquist frequency or folding frequency. If the spectrum $X (f)$ is zero¹³ for $f \in [F_{s} ∕ 2, \infty [$ , then the values of $X (ω)$ in the range $2 π \times [- F_{s} ∕ 2, F_{s} ∕ 2]$ coincides with the values of $X (e^{j Ω})$ normalized by $F_{s}$ in the corresponding range of $[- π, π]$ . In other words:

X (e^{j Ω}) = F_{s} X (ω),

which will be proved later on. Note that $X (e^{j Ω}) = F_{s} X (ω)$ only holds if the sampling theorem is obeyed, otherwise the components of signal $x (t)$ with frequencies in the range $] - \infty, F_{s} ∕ 2 [$ and $] F_{s} ∕ 2, \infty [$ will be mapped (or folded, which is the reason for calling $F_{s} ∕ 2$ the folding frequency) to components of $x [n]$ with angular frequencies in the range $] - π, π [$ , eventually distorting the discrete-time representation of the original $x (t)$ . This phenomenon is called aliasing because a folded component from $X (ω)$ appears in $X (e^{j Ω})$ as an “alias” or impostor.

Figure 2.19: Spectrum $X (f)$ (top) and $X (e^{j Ω})$ when $F_{s} = 60$ Hz. The two indicated points are related by $ω = Ω F_{s}$ and the frequency $f = 6.238$ Hz is mapped into $Ω = 0.6532$ rad. Notice three of the infinite number of replicas of $X (f)$ centered at $Ω \in [- 2 π, 0, 2 π]$ . In this case there was no aliasing because the sampling theorem was obeyed.

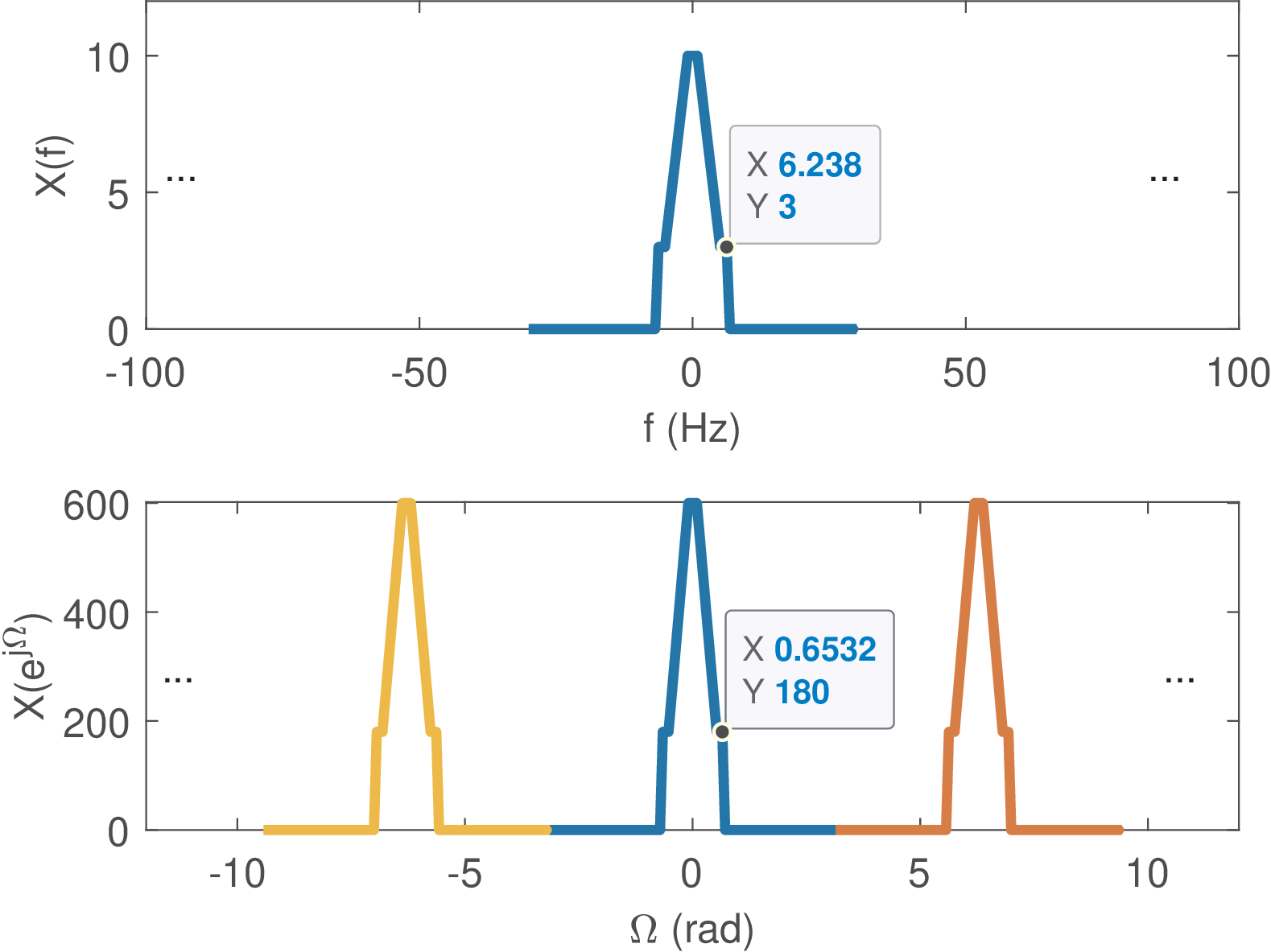
For the sake of illustration, Figure 2.19 depicts the spectrum $X (f)$ of a continuous-time signal $x (t)$ . It also shows the spectrum $X (e^{j Ω})$ of $x [n]$ , obtained by sampling $x (t)$ with $F_{s} = 60$ Hz. In this case, $ω = 2 π \times 6.238$ rad/s is mapped to $0.6532$ rad, with the magnitude being scaled by 60, according to $X (e^{j Ω}) = F_{s} X (ω)$ . This discussion aims at illustrating how the Fourier transform $X (f)$ of $x (t)$ and the DTFT of the corresponding $x [n]$ (obtained from $x (t)$ via a C/D conversion) are related. The next paragraphs complement Eq. (2.35) and discuss how to interpret the DFT in Hz.

¹³ More strictly, only the magnitude matters: the condition is $| X (f) | = 0, f \geq F_{s} ∕ 2$ because the phase can be discarded when the magnitude is zero.