2.2  Linear Transform

The goal in this section is to analyze a signal ($x(t)$ or $x[n]$) using a linear transform. The following steps will be discussed:

f 1.

We will choose the linear transform.

f 2.

The linear transform will represent the signal using its basis functions, which are often orthogonal among themselves.

f 3.

The transform operation corresponds to finding the values called transform coefficients, which multiplied by the corresponding basis functions (one coefficient per basis functions) reconstruct the original signal.

To fully understand linear transforms, we will discuss these concepts using vectors and linear algebra. Later we will generalize from vectors to signals. We start this study of linear transform, associating it to a simple matrix multiplication.

2.2.1  Matrix multiplication corresponds to a linear transform

In linear algebra, any linear transformation¹ (or transform) can be represented by a matrix $\mathbf{\text{A}}$. The linear transform operation is given by

where $\mathbf{\text{x}}$ and $\mathbf{\text{y}}$ are the input and output column vectors, respectively.

Example 2.1. Example of linear transform. The matrix

implements a transform that corresponds to a clockwise rotation of the input vector by an angle $𝜃$.

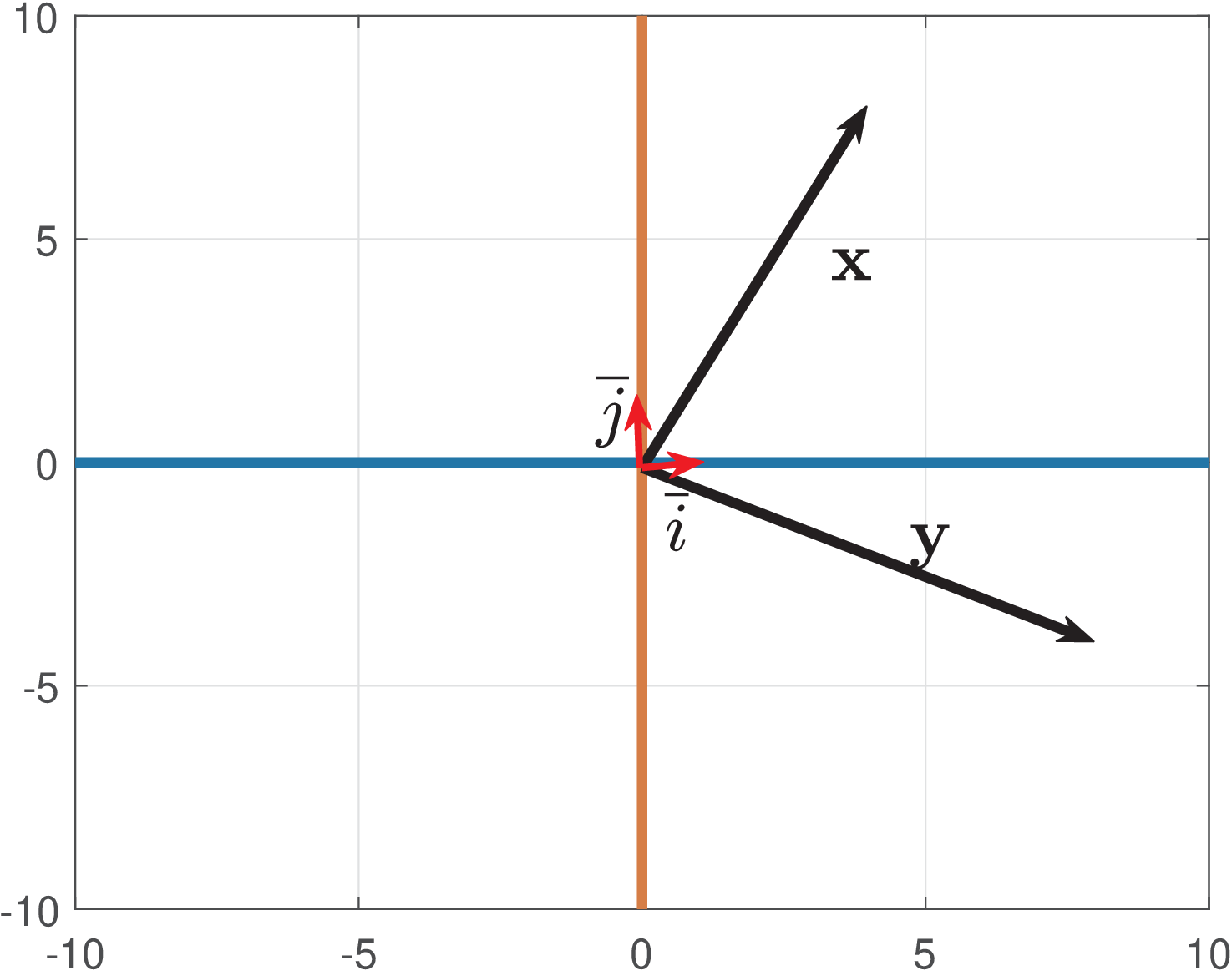
Figure 2.1 illustrates the rotation for a vector $\mathbf{\text{x}}={[4,8]}^T$ by an angle $𝜃=\pi ∕2$ radians, i. e., $\mathbf{\text{A}}=[0,1;-1,0]$, resulting in $\mathbf{\text{y}}=\mathbf{\text{A}}\mathbf{\text{x}}={[8,-4]}^T$.    $\text{□}$

2.2.2  Basis: standard, orthogonal and orthonormal

Another important concept in linear transforms, which has origin in linear algebra, is the concept of basis. The linear combination of basis vectors allow to create any possible vector in the corresponding vector space. Many basis are orthogonal or orthonormal. Figure 2.1 indicates a pair of orthonormal² vectors $\overline{i}=[1,0]$ and $\overline{j}=[0,1]$ that span ${ℝ}^2$. The vectors $\overline{i}$ and $\overline{j}$ form a standard basis and allow to easily represent any vector $\mathbf{\text{y}}\in {ℝ}^2$, such as $\mathbf{\text{y}}=8\overline{i}-4\overline{j}$. It is useful to get a geometric interpretation by studying basis vectors, and later generalize the concepts to basis functions that represent discrete or continuous-time signals.

When the basis vectors are organized as the columns of a matrix $\mathbf{\text{A}}$, the elements of the input vector $\mathbf{\text{x}}$ indicate the coefficients of a linear combination of the basis functions that leads to $\mathbf{\text{y}}$. For example, in the case of the standard basis:

which is a trivial relation because $\mathbf{\text{A}}$ is the identity matrix. More interesting transforms are used in practice.

Example 2.2. Interpreting the given example as a linear transform. Assume one is dealing with computer graphics and wants to rotate vectors. Eq. (2.2) of Example 2.1 with $𝜃=\pi ∕2$ radians leads to (see Figure 2.1):

This can be interpreted as a transform as follows:

f 1.

We chose $\mathbf{\text{A}}$ with $𝜃=\pi ∕2$ as the linear transform.

f 2.

In this case, the elements of $\mathbf{\text{y}}$ are interpreted as the transform coefficients, while $\mathbf{\text{x}}$ is interpreted as the original vector.

The forward transform operation corresponds to finding the coefficients to compose $\mathbf{\text{y}}$. In the inverse operation, the coefficients $\mathbf{\text{y}}$ would be the input values, and $\mathbf{\text{x}}$ could be found using $\mathbf{\text{x}}={\mathbf{\text{A}}}^{-1}\mathbf{\text{y}}$. In practice, we avoid the task of inverting a matrix and often choose $\mathbf{\text{A}}$ with special properties. For instance, because the columns of $\mathbf{\text{A}}$ are orthonormal, its inverse ${\mathbf{\text{A}}}^{-1}={\mathbf{\text{A}}}^H$ is equal to its Hermitian (and the basis vectors are the rows of $\mathbf{\text{A}}$). Tricks to avoid inverting matrices will be further explored, alongside with the adoption of inner products.   $\text{□}$